A water hose is used to fill a large cylindrical storage tank of diameter $D$ and height $2D$. The hose shoots the water at $45^\circ$ above the horizontal from the same level as the base of the tank and is a distance $6D$ away. For what range of launch speeds $v_0$ will the water enter the tank. Ignore air resistance.
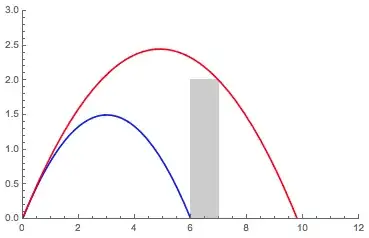
I've made a graphic representing the problem (with $D=1$) showing the trajectory of the water at the minimum launch speed $v_{0\text-m}$ (blue) and maximum launch speed $v_{0\text-M}$ (red) as well as the tank (light gray):
Clearly I've made a mistake in solving for the minimum launch speed - I expect the blue parabola to intersect the rectangle at its top left vertex. I'm not sure where the mistake lies, because as far as I can tell I've used the same approach to solve for $v_{0\text-m}$ as I had for $v_{0\text-M}$, which I'll show first.
The position vector for water particles escaping the hose has components
$$\begin{cases} x=v_{0\text-M}\cos45^\circ t\\ y=v_{0\text-M}\sin45^\circ t-\frac g2t^2 \end{cases}$$
With $x=7D$, solve for $t$ in the first equation, substitute into the second with $y=2D$ to get
$$t=\frac{7D}{v_{0\text-M}\cos45^\circ}\implies2D=v_{0\text-M}\sin45^\circ\left(\frac{7D}{v_{0\text-M}\cos45^\circ}\right)-\frac g2\left(\frac{7D}{v_{0\text-M}\cos45^\circ}\right)^2$$
$$\implies5=\frac{49Dg}{v_{0\text-M}^2}\implies v_{0\text-M}=7\sqrt{\frac{Dg}5}$$
Now to find $v_{0\text-m}$, the only change in the work above - I would think - would be to set $x=6D$.
$$t=\frac{6D}{v_{0\text-m}\cos45^\circ}\implies2D=v_{0\text-m}\sin45^\circ\left(\frac{6D}{v_{0\text-m}\cos45^\circ}\right)-\frac g2\left(\frac{6D}{v_{0\text-m}\cos45^\circ}\right)^2$$
$$\implies2=\frac{12Dg}{v_{0\text-m}^2}\implies v_{0\text-m}=\sqrt{6Dg}$$
Manipulating the code for the plot of the blue parabola, it would appear the correct answer for $v_{0\text-m}$ is closer to $3\sqrt{Dg}$. How can I salvage my attempt to obtain the right solution?