Imagine we have a linear or affine space of real symmetric $n\times n$ matrices: $$\mathcal{A}=\{A_0+c_1 A_1+\ldots+c_m A_m: c\in \mathbb{R}^m\}$$ The question is how to efficiently test if it contains matrix of given eigenspectrum? Equivalently: of given characteristic polynomial?
Trying to expand characteristic polynomial, we get exponential number of terms - the question is if we can test it in polynomial time in $n, m$ e.g. with some numerical procedure?
Examples of eigenspectrum for 1D linear space of $4\times 4$ matrices:
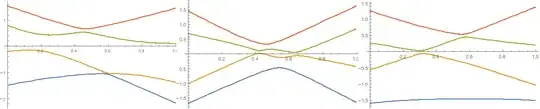
My motivation is that such test is one of two missing links (second) for testing graph isomorphism in polynomial time: looking at eigenspaces of adjacency matrix, we can transform the problem into question if two sets of points differ only by rotation - e.g. 16 points in 6D forming very regular polyhedron. I wanted to describe this set as $\{x:x^T A x=1\textrm{ for all } A\in\mathcal{A}\}$ intersection of ellipsoids. Having such description for both sets, we could test if they differ by rotation using characteristic polynomial - leading to the test from this question.
Update: Here is a useful estimation (but no source?), which should allow for a numerical procedure (e.g. some interleaving steps of QR algorithm and mixing of matrices):
A simple estimate which is often useful is that, if $A$ and $B$ are Hermitian matrices with eigenvalues $a_1 > a_2 > \ldots > a_n$ and $b_1 > b_2 > \ldots > b_n$ and the eigenvalues of the sum are $c_1 > c_2 > \ldots > c_n$, then
$$ c_{i+j-1} \le a_i + b_j \quad\text{and}\quad c_{n-i-j} \ge a_{n-i} + b_{n-j}. $$