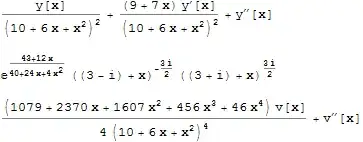Does Heun's differential equation have other known types confluent approach?

Question

We know that the Heun's differential equation is

$\dfrac{d^2y}{dx^2}+\left(\dfrac{\gamma}{x}+\dfrac{\delta}{x-1}+\dfrac{\epsilon}{x-a}\right)\dfrac{dy}{dx}+\dfrac{\alpha\beta x-q}{x(x-1)(x-a)}y=0$ , where $\epsilon=\alpha+\beta-\gamma-\delta+1$ .

How about the other issues e.g.

$\dfrac{d^2y}{dx^2}+\left(\dfrac{\gamma}{x}+\dfrac{\delta}{x-1}+\dfrac{\epsilon}{x^2}\right)\dfrac{dy}{dx}+\dfrac{\alpha\beta x-q}{x^2(x-1)}y=0$

$\dfrac{d^2y}{dx^2}+\left(\dfrac{\gamma}{x}+\dfrac{\delta}{x-1}+\dfrac{\epsilon}{(x-1)^2}\right)\dfrac{dy}{dx}+\dfrac{\alpha\beta x-q}{x(x-1)^2}y=0$

$x^3\dfrac{d^2y}{dx^2}+(ax^2+bx+c)\dfrac{dy}{dx}+(px+q)y=0$

@Robert Israel The first two consider $a\to0$ and $1$ respectively — doraemonpaul, Aug 15 '17 at 16:24
@doraemonpaul I am sorry but I cannot see how do you obtain the second case from taking $a \rightarrow 0$ in the first one? How do you generate the $\epsilon/x^2$ term? — Przemo, Mar 07 '23 at 12:32
@doraemonpaul In which book did you find the case in which a=1? I found this equation and I'm trying to find its relation with the general heun eq. Thanks — Jmtz, Dec 14 '23 at 14:39

score 0 · Answer 1 · answered Oct 24 '18 at 18:09

Unfortunately this is not an answer to your question but I have found another broad class of ODEs, similar to those above, which are solved in terms of the doubly-confluent Heun functions. They are: \begin{equation} \left(p_2+q_2 x+r_2 x^2\right)^2 y^{''}(x) + \left(p_1 + q_1 x\right) y^{'}(x) + p_0 y(x)=0 \end{equation} where both $p_2\neq 0$ and $q_1 \neq 0$ and $p_0 \neq 0$. By eliminating the coefficient at the 1st derivative, i.e. by writing: \begin{equation} y(x)=\exp\left(-\frac{1}{2} \int \frac{\left(p_1 + q_1 x\right)}{\left(p_2+q_2 x+r_2 x^2\right)^2} dx \right) \cdot v(x) \end{equation}

they are always reduced to the following ODE: \begin{eqnarray} v^{''}(x) + \frac{{\mathfrak P}_0+{\mathfrak P}_1 x + {\mathfrak P_2} x^2 + {\mathfrak P_3} x^3 + {\mathfrak P_4} x^4}{(p_1 x+q_1)^4 (p_2 x+q_2)^4} \cdot v(x)=0 \end{eqnarray} which in turn can be always solved in terms of the doubly confluent Heun functions as demonstrated in Algorithm for solving a large class of linear 2nd order ODEs with polynomial coefficients. .

See the following Mathematica code snippet for the illustration of that:

{p0, q0, r0} = RandomInteger[{1, 10}, 3];
{p1, q1, r1} = RandomInteger[{1, 10}, 3];
{p2, q2, r2} = RandomInteger[{1, 10}, 3];
Clear[y]; x =.; Clear[v];
myeqn = (p2 + q2 x + r2 x^2)^2 y''[x] + (p1 + q1 x) y'[x] + (p0) y[x];
myeqn = Collect[
  myeqn/Coefficient[myeqn, y''[x]], {y[x], y'[x], y''[x]}, Simplify]
mycoeff = Coefficient[myeqn, y'[x]];
myparam = Coefficient[PowerExpand[Sqrt[Denominator[mycoeff]]], x^2]^2;
m[x_] = Simplify[
  Exp[Total[(-1/2) Integrate[
      List @@ Apart[
        Numerator[
          mycoeff]/(myparam Times @@ (x - # & /@ (x /. 
                Solve[Denominator[mycoeff] == 0, x]))), x], x]]]]
y[x_] = m[x] v[x];
Collect[Simplify[myeqn/m[x]], {v[x], v''[x]}, Simplify]

score 0 · Answer 2 · answered Nov 21 '18 at 17:45

Again, this is not exactly an answer to your question but I found exact solutions to an ODE very similar to the one on the bottom of your question. Define: \begin{eqnarray} p&:=&\frac{b_1}{4}(-2+a_1-c_1)\\ q&:=&\frac{a_1+c_1}{4}(-2+a_1-c_1) \end{eqnarray} and consider the following ODE: \begin{eqnarray} x(x-1)(x+1) \frac{d^2 y(x)}{d x^2} + \left( a_1 x^2+b_1 x+c_1\right) \frac{d y(x)}{d x} + (p+q x) y(x)=0 \end{eqnarray} Then we have: \begin{eqnarray} y(x):=\frac{1}{m(x)} \left( C_1 F_{2,1} \left[ a,b,c,f(x)\right] + C_2 [f(x)]^{1-c} F_{2,1}\left[a+1-c,b+1-c,2-c,f[x]\right]\right) \end{eqnarray} where \begin{eqnarray} m(x)&:=& x^{\frac{1}{2} (-c-c_1)} (x+1)^{a+\frac{1}{4} (a_1+4 b-b_1+c_1-2)} (1-x)^{\frac{1}{4} (-4 a+a_1-4 b+b_1+4 c+c_1-2)}\\ f(x)&:=&\frac{4 x}{(x+1)^2} \end{eqnarray} and \begin{eqnarray} \left( \begin{array}{r} a \\ b \\ c \end{array} \right) = \left\{ \left( \begin{array}{r} \frac{1}{4}(2-a_1-3 c_1) \\ \frac{1}{4}(-b_1-2 c_1) \\ -c_1 \end{array} \right), \left( \begin{array}{r} \frac{1}{4}(-2+a_1- c_1) \\ \frac{1}{4}(b_1-2 c_1) \\ -c_1 \end{array} \right) \right\} \end{eqnarray}

In[2]:= a1 =.; b1 =.; c1 =.;
a =.; b =.; c =.; x =.;
f[x_] = 4 x/(x + 1)^2;
m[x_] = (1 - x)^(1/4 (-2 - 4 a + a1 - 4 b + b1 + 4 c + c1)) x^(
   1/2 (-c - c1)) (1 + x)^(a + 1/4 (-2 + a1 + 4 b - b1 + c1));

{p, q} = { b1 (-2 + a1 - c1), (-2 + a1 - c1) (a1 + c1)}/4;
a = {1/4 (2 - a1 - 3 c1), 1/4 (-2 + a1 - c1)};
b = {1/4 (-b1 - 2 c1), 1/4 (b1 - 2 c1)};
c = {-c1, -c1};
{b, c} = {(-2 b1 + a1 b1 - 8 a c1 + b1 c1 - 4 c1^2)/(
   8 (2 a + c1)), -c1};
eX = (x (x - 1) (x + 1) D[#, {x, 2}] + (a1 x^2 + b1 x + c1) D[#, 
        x] + (p + q x) #) & /@ {1/
      m[x] (C[1] Hypergeometric2F1[a, b, c, f[x]] + 
       C[2] f[x]^(1 - c) Hypergeometric2F1[a + 1 - c, b + 1 - c, 
         2 - c, f[x]])};


{a1, b1, c1, x} = RandomReal[{0, 1}, 4, WorkingPrecision -> 50];
Simplify[eX]

Out[13]= {{0.*10^-47 C[1] + 0.*10^-48 C[2], 
  0.*10^-47 C[1] + 0.*10^-48 C[2]}}

This is a generalization of example 1.1 in page 3 in https://arxiv.org/abs/1606.01576 .

Does Heun's differential equation have other known types confluent approach?

2 Answers2

Linked