Let $\left\{ {\mathfrak P}_j \right\}_{j=0}^4$ be integers each of which is different from zero. Likewise let $p_1$,$p_2$,$q_1$ and $q_2$ be other integers that too are all different from zero.
From my answer to Looking for closed form solutions to linear ordinary differential equations with time dependent coefficients. we know that every linear ODE of the form: \begin{eqnarray} v^{''}(x) + \frac{{\mathfrak P}_0+{\mathfrak P}_1 x + {\mathfrak P_2} x^2}{(p_1 x+q_1)^2 (p_2 x+q_2)^2} \cdot v(x)=0 \quad (I) \end{eqnarray} is always solved in terms of properly rescaled hypergeometric function .
In here I am going to present an algorithm that solves a more general ODE: \begin{eqnarray} v^{''}(x) + \frac{{\mathfrak P}_0+{\mathfrak P}_1 x + {\mathfrak P_2} x^2 + {\mathfrak P_3} x^3 + {\mathfrak P_4} x^4}{(p_1 x+q_1)^4 (p_2 x+q_2)^4} \cdot v(x)=0 \quad (II) \end{eqnarray} in terms of the doubly-confluent Heun function https://dlmf.nist.gov/31.12 .
The algorithm is as follows.
Consider a properly rescaled doubly-confluent Heun operator: \begin{eqnarray} {\mathfrak L}^{(a,q)}_{\delta,\gamma,e}(x):=\frac{d^2}{d x^2} + \left( \frac{\delta}{x^2} + \frac{\gamma}{x} + e\right) \frac{d}{d x} + \frac{a x-q}{x^2} \end{eqnarray} Note that every doubly confluent Heun operator can be brought into this form by rescaling the independent variable appropriately. Indeed changing $x \rightarrow e \cdot x$ results in ${\mathfrak L}^{(a,q)}_{\delta,\gamma,1}(x) \rightarrow {\mathfrak L}^{(a \cdot e,q)}_{\delta/e,\gamma,e}(x)$.
Generate some random $\left\{ {\mathfrak P}_j \right\}_{j=0}^4 \in {\mathbb N}_+^4$ and another random $(p_1,p_2,q_1,q_2) \in {\mathbb N}_+^4$ and define $(A,B,C,D):=(p_1,q_1,p_2,q_2)$ .
Define five quantities $\left({\mathfrak A}_j\right)_{j=0}^4$ which are quadratic polynomials in the parameters $(\delta,\gamma,e,a,q)$ of the Heun operator . We have:
\begin{eqnarray} {\mathfrak A}_0&:=&-4 a B^3 D+B^4 e^2+g \left(2 B d D^3-2 B^2 D^2\right)+B^2 D^2 g^2+4 B^2 D^2 q+e \left(2 B^3 D g+2 B^2 d D^2\right)-4 B d D^3+d^2 D^4\\ {\mathfrak A}_1&:=&-4 a B^2 (3 A D+B C)+4 A B^3 e^2+e \left(2 B^2 g (3 A D+B C)+4 B d D (A D+B C)\right)+g \left(2 d D^2 (A D+3 B C)-4 B D (A D+B C)\right)-4 d D^2 (A D+3 B C)+2 B D g^2 (A D+B C)+8 B D q (A D+B C)+4 C d^2 D^3\\ {\mathfrak A}_2&:=&-12 a A B (A D+B C)+e \left(2 d \left(A^2 D^2+4 A B C D+B^2 C^2\right)+6 A B g (A D+B C)\right)+g \left(6 C d D (A D+B C)-2 \left(A^2 D^2+4 A B C D+B^2 C^2\right)\right)+g^2 \left(A^2 D^2+4 A B C D+B^2 C^2\right)+4 q \left(A^2 D^2+4 A B C D+B^2 C^2\right)+6 A^2 B^2 e^2-12 C d D (A D+B C)+6 C^2 d^2 D^2\\ {\mathfrak A}_3&:=&-4 a A^2 (A D+3 B C)+4 A^3 B e^2+e \left(2 A^2 g (A D+3 B C)+4 A C d (A D+B C)\right)+g \left(2 C^2 d (3 A D+B C)-4 A C (A D+B C)\right)-4 C^2 d (3 A D+B C)+2 A C g^2 (A D+B C)+8 A C q (A D+B C)+4 C^3 d^2 D\\ {\mathfrak A}_4&:=&-4 a A^3 C+A^4 e^2+A^2 C^2 g^2+4 A^2 C^2 q+g \left(2 A C^3 d-2 A^2 C^2\right)+e \left(2 A^3 C g+2 A^2 C^2 d\right)-4 A C^3 d+C^4 d^2 \end{eqnarray} and solve a system of five coupled quadratic equations $\left({\mathfrak A}_j\right)_{j=0}^4=\left(4{\mathfrak P}_j\right)_{j=0}^4$ for the five parameters of the Heun operator.
- Define the following functions: \begin{eqnarray} f(x)&:=& \frac{A x + B}{C x+D}\\ m(x)&:=& f(x)^{-g/2} \sqrt{f'(x)} e^{\frac{d}{2 f(x)}-\frac{1}{2} e f(x)} \end{eqnarray}
Then the function: \begin{equation} v(x):= \frac{y(f(x))}{m(x)} \end{equation} satisfies the ODE $(II)$ subject to $y$ being a solution to \begin{equation} {\mathfrak L}^{(a,q)}_{\delta,\gamma,e}(x)\left[ y(x) \right]= 0 \end{equation}
Below I enclose the implementation of this algorithm in Mathematica:
e =.; g =.; d =.; a =.; q =.; A =.; B =.; CC =.; DD =.; x =.;
{P0, P1, P2, P3, P4} = RandomInteger[{1, 10}, 5];
{p1, p2, q1, q2} = RandomInteger[{1, 10}, 4];
myinput = (P0 + P1 x + P2 x^2 + P3 x^3 +
P4 x^4)/((p1 x + q1)^4 (p2 x + q2)^4)
{A, B, CC, DD} = {p1, q1, p2, q2};
num = -(B CC - A DD)^2 {-4 a B^3 DD - 4 B d DD^3 + d^2 DD^4 +
B^4 e^2 + (-2 B^2 DD^2 + 2 B d DD^3) g + B^2 DD^2 g^2 +
e (2 B^2 d DD^2 + 2 B^3 DD g) + 4 B^2 DD^2 q,
4 CC d^2 DD^3 - 4 d DD^2 (3 B CC + A DD) -
4 a B^2 (B CC + 3 A DD) +
4 A B^3 e^2 + (-4 B DD (B CC + A DD) +
2 d DD^2 (3 B CC + A DD)) g + 2 B DD (B CC + A DD) g^2 +
e (4 B d DD (B CC + A DD) + 2 B^2 (B CC + 3 A DD) g) +
8 B DD (B CC + A DD) q,
6 CC^2 d^2 DD^2 - 12 a A B (B CC + A DD) -
12 CC d DD (B CC + A DD) +
6 A^2 B^2 e^2 + (6 CC d DD (B CC + A DD) -
2 (B^2 CC^2 + 4 A B CC DD + A^2 DD^2)) g + (B^2 CC^2 +
4 A B CC DD + A^2 DD^2) g^2 +
e (2 d (B^2 CC^2 + 4 A B CC DD + A^2 DD^2) +
6 A B (B CC + A DD) g) +
4 (B^2 CC^2 + 4 A B CC DD + A^2 DD^2) q,
4 CC^3 d^2 DD - 4 a A^2 (3 B CC + A DD) -
4 CC^2 d (B CC + 3 A DD) +
4 A^3 B e^2 + (-4 A CC (B CC + A DD) +
2 CC^2 d (B CC + 3 A DD)) g + 2 A CC (B CC + A DD) g^2 +
e (4 A CC d (B CC + A DD) + 2 A^2 (3 B CC + A DD) g) +
8 A CC (B CC + A DD) q, -4 a A^3 CC - 4 A CC^3 d + CC^4 d^2 +
A^4 e^2 + (-2 A^2 CC^2 + 2 A CC^3 d) g + A^2 CC^2 g^2 +
e (2 A^2 CC^2 d + 2 A^3 CC g) + 4 A^2 CC^2 q};
eX = Sum[num[[i + 1]] x^i, {i, 0, 4}]/(4 (B + A x)^4 (DD + CC x)^4) ;
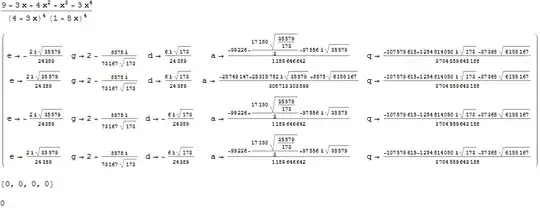
subst = Simplify[
Solve[num == {4 P0, 4 P1, 4 P2, 4 P3, 4 P4}, {e, g, d, a, q}]];
MatrixForm[subst]
Simplify[(eX /. subst) - myinput]
Clear[f]; Clear[m]; Clear[y];
f[x_] = (A x + B)/(CC x + DD);
m[x_] = E^(d/(2 f[x]) - 1/2 e f[x]) f[x]^(-g/2) Sqrt[
Derivative[1][f][x]];
Clear[y];
v[x_] = y[f[x]]/m[x];
{e, g, d, a, q} = {e, g, d, a, q} /. subst[[1]];
FullSimplify[(v''[x] + myinput v[x]) /.
Derivative[2][y][
x_] :> -(d/x^2 + g/(x) + e) y'[x] - (a x - q)/(x^2) y[x]]
Having said all this my question would be the following. Consider now a general linear 2nd order ODE with polynomial coefficients. What constraints should we impose on the coefficients so that the ODE in question can be mapped onto the ODE $(II)$ and therefore solved in terms of the doubly-confluent Heun functions as outlined in this post?