9

The question really is in the title. I know what it means if the dot product equals 0 but I find it interesting thinking what it means when it equals exactly 1 and can't seem to find anything online to enlighten me.

Thanks

moony
  • 780
  • 4
    Nothing special, really. You get some relation between their lengths and to what degree they point in the same direction, but it's not anything really firm. – Arthur Mar 20 '17 at 23:15
  • 2
    I don't think it means anything in particular, but check this post for an intuition about the dot product. – Bobson Dugnutt Mar 20 '17 at 23:15
  • 1
    The value of the dot product has dimensions square length, so it means nothing without a reference pair of lengths to compare it to (namely the lengths of the original vectors) unless it is zero, because this statement does not depend on a choice of units. – Qiaochu Yuan Mar 20 '17 at 23:20
  • Thanks very much. I wish I could accept one of these as answers as you have answered my question. Thanks – moony Mar 20 '17 at 23:47

3 Answers3

6

I'm really surprised this question still doesn't have a complete answer.

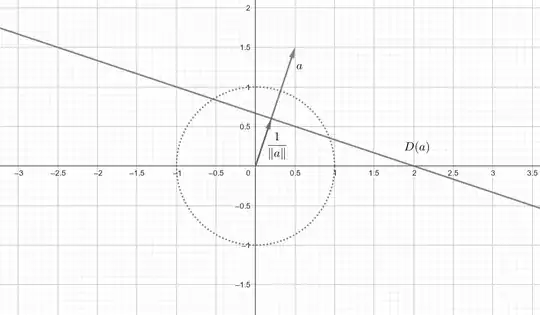
Given any vector $a \in \mathbb{R}^2 \setminus \{0\}$, the set $$D(a) = \left\{x \in \mathbb{R}^2 \mid \left\langle a,x \right\rangle=1\right\}$$ looks like this: Geometric interpretation of the Duality Transform of a vector a

$D(a)$ is a line with distance $\frac{1}{\|a\|}$ from the origin perpendicular to $a$.

If you move $a$ to the unit circle (indicated with a dotted line), $D(a)$ will be tangent to the unit circle at $a$. If you know that $x$ is pointing in the same direction as $a$, you can see it has length $\frac{1}{\|a\|}$, as indicated by the other answers.

In the context of discrete geometry, $D(a)$ is also called the Duality Transform of $a$, which makes it a bit tricky to look up, since the concept of duality is everywhere in mathematics. I can't seem to find this term in online sources, but this is what it's called in academic textbooks.

So, to answer the question: if you know two vectors $a$ and $b$ have a dot product of $1$, you know that $b$ is somewhere in the Duality Transform of $a$, and - since the dot product is commutative - that $a$ is in the Duality Transform of $b$.

Side note: this concept generalizes to any dimension. In $\mathbb{R}^3$, $D(a)$ will be a plane with normal vector $a$ and distance $\frac{1}{\|a\|}$ from the origin.

hensing1
  • 61
  • This follows from the fact that each vector is the sum of of a vector parallel to $a$ and a vector perpendicular to $a$, right? – Filippo Oct 29 '24 at 09:47
  • I don't really agree. A point and a line can be the dual of each other in this context. But not two points. [Duality is a very useful concept, as it twins the theorems.] –  Oct 29 '24 at 09:48
  • @YvesDaoust yes, the duality transform is a mapping between the point and the hyperplane (the line, in this case). The point $b$ is contained in the duality transform of $a$, maybe I should have been a bit more concise in the answer. – hensing1 Oct 29 '24 at 09:52
5

If you already know the vectors are both normalized (of length one), then the dot product equaling one means that the vectors are pointing in the same direction (which also means they're equal).

If you already know the vectors are pointing in the same direction, then the dot product equaling one means that the vector lengths are reciprocals of each other (vector b has its length as 1 divided by a's length). For example, 2D vectors of (2, 0) and (0.5, 0) have a dot product of 2 * 0.5 + 0 * 0 which is 1. Also, (1, 1) has a length of sqrt(2), and (0.5, 0.5) has a length of 1/sqrt(2), and the dot product is also 1.

If you don't already know anything about the vectors, you can't concretely say anything about this.

Aaron Franke
  • 438
  • 2
    Your second statement is false, take the vectors $[1,1]$ and $[1/2,1/2]$; the dot product is $1$ but they are not "reciprocals" – TY Mathers Oct 02 '19 at 01:21
  • @AlexMathers Good catch! That's what I get for not thinking up counterexamples... I think the actual rule is the lengths are reciprocal, I've edited my answer to reflect this. – Aaron Franke Oct 02 '19 at 01:36
0

Unless the vectors are normalized or the context is a geometric inversion, the dot product being equal to $1$ is essentially coincidental and has no useful meaning.

If they are normalized, then they are parallel. $-1$ for antiparallel.

  • Why this downvote? –  Oct 29 '24 at 09:49
  • 1
    I agree with your answer (+1)! Fix a pair of vectors. Unless the dot product is equal to zero, we can always choose the unit of length such that the dot product equals 1. So the question is: What can we say if the product is non-zero? And the answer is that the dot product is zero if and only if one vector is equal to zero or the vectors are perpendicular. – Filippo Oct 29 '24 at 10:52
  • @Filippo: thank you for the support, but this did not prevent three unexplained downvotes. –  Oct 29 '24 at 10:58