How many squares are crossed by the diagonal of a rectangle splitted into $N \times M$ squares

Question

I need help with this question

Here is the problem: I have a rectangle with fixed size NxM, such that N, M are positive natural numbers. And this rectangle of size NxM is splitted into squares with size 1x1 ; actually if the rectangle sizes are 3x3, it is splited into 9 squares. This picture is showing 4 variants.

And actually the picture is also showing the thing i want to find, the number of small squares crossed by the diagonal of the rectangle. In all 4 variants it is passing through 4 squares.

Thanks in advance.

Answer 1

First, suppose that $N$ and $M$ have no common factor. Then the diagonal line doesn't go through any intersections, so each time it crosses a horizontal or vertical grid line, it adds $1$ to the number of squares touched. And to get from the top left to the bottom right, it must pass through $N-1$ vertical grid lines and $M-1$ horizintal grid lines. Counting the orginal square in the top left, this gives a total of $1+(N-1)+(M-1)=N+M-1$ squares touched. This formula applies to your first and second diagrams.

Now suppose that $N$ and $M$ have a common factor. Let $q=(N,M)$ be the largest common factor of $N$ and $M$. Then $N/q$ and $M/q$ have no common factor, so we can break the problem up into $q$ smaller rectangles strung along the diagonal, each of size $N/q\times M/q$; and in each such rectangle the number of squares visited is $N/q+M/q-1$. So the total number of squares visited is $q\times(N/q+M/q-1) = N+M-q$.

Hence in all cases the number of squares touched is

$$N+M-(N,M)$$

Answer 2

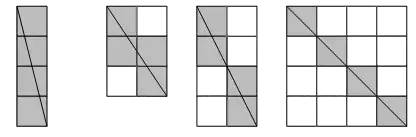
The crux of solving this problem is in the fact that, the diagonal cutting a vertical line enters in one unique square, and when it cuts a vertical line enters another unique square.

Case 1: $N/M$ is irreducible

Draw them yourself and be convinced with that fact! And then the total number will emerge by adding $N-1$ vertical lines $=$ $N-1$ unique squares, and $M-1$ horizontal lines = $M-1$ unique squares, but the first square is where we started and it was not counted therefore $(N-1)+(M-1)+1 = N+M-1$ is the usual answer, if $N,M$ has no common factor.

The usual confusing point is how come common factor is related to diagonal don't touch any vertices of any of the inside squares.

This can be understood using the slope, taking $s = N/M$, if this is an irreducible rational number than by taking $M$ steps horizontally, you will meet only the vertex at the very last.

Another meaning of this is the following: Only $s \times M$ can produce a natural number $N$, and no other number less than $N$.

Meeting of a interior vertex of a square is not possible because this would mean there exists a number $K<M$ when multiplied to $s$ produces a natural number. Which is in contradiction with the irreducibility of the given $N/M$. And the geometric meaning is that the slope is changed! Which is again not possible! Slope of a straight line remains the same!

Case 2: $N/M$ is reducible

Then for this case, $s = N/M=n/m$ , which means there are interior vertices which the diagonal cuts. Hence the problem is reduced to a case of smallest irreducible $n\times m$ rectangle. Following the same argument from the slope, as it is the same throughout the diagonal, you will reached the top right vertex of the vertical $n$ square, if you walked $m$ squares to the right! And then apply the same $m+n-1$ and then multiply it by $GCD(N,M)$ to get the actual number of squares cut by the diagonal for the $N\times M$ rectangle.

$$n(Sq.)=GCD(N,M)(m+n-1)$$

The $GCD(N,M)$ is basically a multiplication factor, which you will be able to obtain without the need for the jargon $GCD$. It is just the number of the same small rectangles $n\times m$ arranged diagonally to get how it would have appeared if there was $N\times M$ rectangle.