4

How many boxes are crossed by a diagonal in a rectangular table formed by $199 * 991$ small squares ?

Well, the answer is $a+b-\gcd(a, b)$. but, How can I prove that? I tried drawing different diagram. But the only improvement I saw is $f(a, b) = c*f(a/c, b/c)$ where $c$ is $\gcd(a, b)$.

dxiv
  • 77,867
Shakil Ahamed
  • 167
  • 2
    HINTS: How many horizontal lines does the diagonal cross? How many vertical lines? How many times does the diagonal cross a horizontal line and a vertical line at the same point (that is at the small square's vertex)? – CiaPan Nov 13 '15 at 15:21
  • 3
    @CiaPan You should post that as an answer... ;) – A.P. Nov 13 '15 at 17:54
  • @A.P. Possibly you're right. :) As nobody else answered, I did it. – CiaPan Nov 13 '15 at 23:34
  • @GermainWest Please don't make gratuitous changes to other users' posts. I rolled the edit back. If they had meant to use spoilers, they would have done it themselves. – dxiv Jul 04 '22 at 01:03

1 Answers1

5

For a rectangle of size $m\times n$ with sizes being coprime:

  • when a diagonal leaves the starting corner, it goes through the first square;
  • and before it reaches the opposite corner it crosses $n-1$, say, horizontal lines of the grid, and $m-1$ vertical lines, each time entering a new square.

So the diagonal visits $m+n-1$ unit squares.

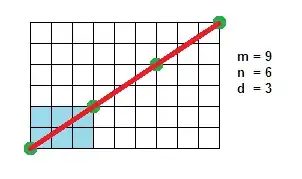
For sizes not coprime let $d = \gcd(m,n)$. Then we can reduce the problem to $d$ rectangles of size $\frac md\times\frac nd$ which makes a result of $$d\cdot \left(\frac md + \frac nd - 1\right) = m + n - d$$ $$ = m + n - \gcd(m,n)$$

And we can see, that the former result is a special case of the latter: the 'minus one' term is a 'minus GCD of sizes', since a GCD of coprime numbers is $1$.

CiaPan
  • 13,884
  • This is a bit imprecise. There are $d^2$ rectangles of size $m/d \times n/d$ in a $m \times n$ grid. It is true, though, that the diagonal crosses only $d$ of them. – A.P. Nov 14 '15 at 10:03
  • 1
    It doesn't matter how many rectangles one can find in a grid. What's important here is that there are $d$ congruent parts of the grid, containing $d$ equal parts of the diagonal, so we can use a previous, simpler case to solve (each) one $d$-th part of a problem and then compose them into a final answer. The remaining parts of the big rectangle have nothing to do with the solution. – CiaPan Nov 14 '15 at 15:01
  • I'm sorry if I wasn't clear before. I'm not criticising the mathematical content of your answer, I'm just saying that "[t]hen we can reduce the problem to $d$ rectangles of size $m/d \times n/d$" suggests (at least to me) that you are subdividing the original grid in $d$ rectangles of size $m/d \times n/d$, which is not the case. From the answer it isn't clear where the fact that there are $d$ rectangles comes from, which you then explained in your comment. – A.P. Nov 14 '15 at 15:17
  • 2
    @A.P. Hopefully the image I added explains better than words what I meant by 'reducing the problem to $d$ parts'. – CiaPan Nov 23 '15 at 11:11
  • @CiaPan "So the diagonal visits $m+n−1$ unit squares".How did you conclude this? – Wolgwang Jan 21 '21 at 10:29
  • 1
    @YouKnowMe 'it crosses $n−1$ (...) lines of the grid, and $m−1$ (...) lines, each time entering a new square' – so it enters $(n−1)+(m−1)$ squares, which is $(n+m–2)$. Add the initial one, et voilà. – CiaPan Jan 21 '21 at 20:10