2

How would you show that, if $$\mathbf r = \mathbf A \sin \theta + \mathbf B \cos \theta$$ where $\mathbf A$ and $\mathbf B$ are arbitrary constant vectors in $\Bbb R^2$,

then $\mathbf r$ may be written as, $$\mathbf r = \mathbf a \sin (\theta + \alpha) + \mathbf b \cos (\theta + \alpha)$$ for some constant orthogonal vectors $\mathbf a$ and $\mathbf b$ in $\Bbb R^2$, and real constant $\alpha$.

[If it helps: Note that an explicit expression for $\mathbf a$ and $\mathbf b$ is not necessarily needed, just proof of their existence.]

John Don
  • 1,189
  • Orthogonal to what? – Brevan Ellefsen Feb 08 '17 at 01:15
  • He wants $a,b$ to be orthogonal to each other. – Faraad Armwood Feb 08 '17 at 01:16
  • To each other (i.e. independent)... also should clarify, this is all in R^2... not that it makes too much difference – John Don Feb 08 '17 at 01:17
  • I know you probably want to undestand the geometric meaning of that parametrization, but what if you simply set $\textbf{a}=\textbf{r}(\frac{\pi}{2} - \alpha)$, $\textbf{b}=\textbf{r}(-\alpha)$ and the angle $\alpha$ fulfilling the condition $\langle \textbf{a}, \textbf{b} \rangle = 0$? – Matteo Feb 08 '17 at 03:09

2 Answers2

2

Let $\boldsymbol{x}= \begin{pmatrix} \cos \theta \\ \sin \theta \end{pmatrix} \in S^1$

\begin{align*} \boldsymbol{x}^T \boldsymbol{x} &= 1 \\ \boldsymbol{y} &= \begin{pmatrix} \boldsymbol{a} & \boldsymbol{b} \end{pmatrix} \begin{pmatrix} \cos \theta \\ \sin \theta \end{pmatrix} \\ \boldsymbol{y}^T \boldsymbol{y} &= \boldsymbol{x}^T \begin{pmatrix} \boldsymbol{a} \cdot \boldsymbol{a} & \boldsymbol{a} \cdot \boldsymbol{b} \\ \boldsymbol{b} \cdot \boldsymbol{a} & \boldsymbol{b} \cdot \boldsymbol{b} \end{pmatrix} \boldsymbol{x} \end{align*}

Eigenvalues:

$$\lambda_{min} \le \boldsymbol{y}^T \boldsymbol{y} \le \lambda_{max}$$

$$ \frac{a^2+b^2-\sqrt{(a^2-b^2)^2+4(\boldsymbol{a} \cdot \boldsymbol{b})^2}}{2} \le \boldsymbol{y}^T \boldsymbol{y} \le \frac{a^2+b^2+\sqrt{(a^2-b^2)^2+4(\boldsymbol{a} \cdot \boldsymbol{b})^2}}{2}$$

Eigenvectors:

$$\boldsymbol{\alpha}= \boldsymbol{a} \cos \left( \frac{1}{2} \tan^{-1} \frac{2\boldsymbol{a} \cdot \boldsymbol{b}}{a^2-b^2} \right)+ \boldsymbol{b} \sin \left( \frac{1}{2} \tan^{-1} \frac{2\boldsymbol{a} \cdot \boldsymbol{b}}{a^2-b^2} \right)$$

$$\boldsymbol{\beta}= \boldsymbol{b} \cos \left( \frac{1}{2} \tan^{-1} \frac{2\boldsymbol{a} \cdot \boldsymbol{b}}{a^2-b^2} \right)- \boldsymbol{a} \sin \left( \frac{1}{2} \tan^{-1} \frac{2\boldsymbol{a} \cdot \boldsymbol{b}}{a^2-b^2} \right)$$

In general, the angle will be distorted and the sense of rotation may not be preserved: $$\boldsymbol{y}= \boldsymbol{\alpha} \cos (\phi+\phi_0) \pm \boldsymbol{\beta} \sin (\phi+\phi_0)$$

See another answer here.

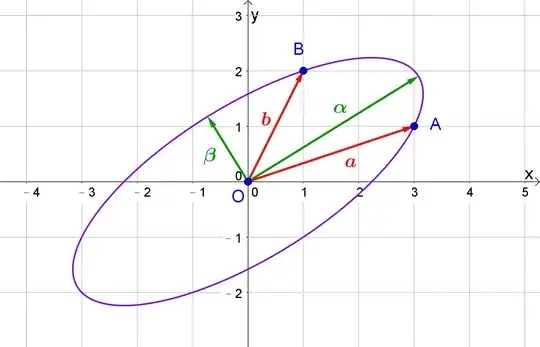
enter image description here

Ng Chung Tak
  • 19,693
1

The first expression can be seen as the product of a $2\times2$ matrix by the vector $(\sin\theta,\cos\theta)$.

By the Eigen decomposition theorem, the matrix can be decomposed in the product of

  • a rotation (of angle $\alpha$),
  • an anisotropic scaling along the coordinate axis,
  • the counter-rotation (of angle $-\alpha$).

The first rotation transforms the vector $(\sin\theta,\cos\theta)$ into $(\sin(\theta+\alpha),\cos(\theta+\alpha))$. The scaling makes a linear combination of two orthogonal vectors of lengths $\|a\|$ and $\|b\|$, hence $(\|a\|\sin(\theta+\alpha),\|b\|\cos(\theta+\alpha))$. The counter rotation gives a new direction to these vectors.

So $\alpha$ corresponds to the directions of the Eigenvectors, which are also the directions of $\mathbf a$ and $\mathbf b$, and the lengths of these vectors are the Eigenvalues.

Alternatively:

Using the angle addition formulas, the two representations are linear combinations of the sine and cosine of $\theta$.

The vectors $\mathbf A$ and $\mathbf B$ carry four degrees of freedom. The vectors $\mathbf a$ and $\mathbf b$ are lacking one, as they are constrained to be orthogonal; but the missing degree of freedom is now supported by the parameter $\alpha$.