This post was posing the question "The Calippo™ popsicle has a specific shape ... Does this shape have an official name?", and the accepted answer was that it is a Right Conoid which in fact is much resembling.
However, a conoid is not developable and so cannot be economically made out of a cardboard sheet.
Now, a cardboard cylinder, pinched and sealed at one end, will look like a toothpaste tube, and the
pinched end will be larger than the mouth diameter (by $\pi /2 $).
That does not fit to the calippo's look,
whose tube is in fact fabricated from a cone (made from a plane circular sector) pinched at one end (and reinforced at the opposite circular rim).
And a related subject is that, a cylinder with both ends pinched at 90° relative to each other make up
a tetrahedral "milk carton" (berlingot in French).
In this Mathcurve page after stating that
"le berlingot est la surface réglée non développable .. ",
referring to a picture of a real tetrahedral milk carton is noted:
"Attention, un berlingot comme ci-dessus fabriqué avec du papier
est une surface développable, fabriquée avec un patron de tétraèdre en arrondissant les arêtes... "
Also refer to the Coin Conic page.
Suppose that the material is inextensible, and that a grid of directrices and orthogonal circles is marked on the cone/cylinder,
then it is clear that upon pinching the directrices will not appear straight.
Since a developable surface implies that it be ruled, then either the ruling lines have moved, or the surface has undergone some deformation.
Therefore the question is:
Can the calippo (and bottom of toothpaste, and milk) package be a ruled developable surface , in case, admitting that the shape of the pinched edge be not exactly linear ? or is some deformation of the material demanded ?
---- P.S: -----
Thanks to the answer, with expressive sketch, received by Rahul, complemented with that provided by C.Blatter to the previous post, we can conclude that such a surface is a plausible model.
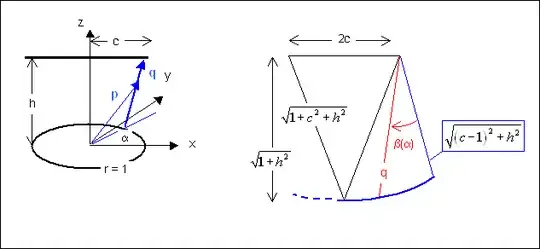
So, scaling all the dimensions to have the base circle of radius $1$, height $=h$ and length of the pitch $=2c$
we can parametrise the surface as $$ \eqalign{ & {\bf q} = \left( {sc,\;0,h} \right) - \left( {\cos \alpha ,\;\sin \alpha ,0} \right) = \left( {sc - \cos \alpha ,\; - \sin \alpha ,h} \right) \cr & {\bf p} = \left( {\cos \alpha ,\;\sin \alpha ,0} \right) + t\,{\bf q} \cr} $$ where $$ \left\{ \matrix{ \alpha = - \pi /2\quad - 1 < s < 1\quad 0 \le t \le 1 \hfill \cr - \pi /2 < \alpha < \pi /2\quad s = 1\quad 0 \le t \le 1 \hfill \cr \alpha = \pi /2\quad - 1 < - s < 1\quad 0 \le t \le 1 \hfill \cr \pi /2 < \alpha < 3\pi /2\quad s = - 1\quad 0 \le t \le 1 \hfill \cr} \right. $$
Then we can develop half of the surface as indicated, by putting for the flattened conic part that $$ q(\alpha )d\beta (\alpha ) = d\alpha \quad \left| \matrix{ \,q = \left| {\bf q} \right| \hfill \cr \,s = 1 \hfill \cr} \right. $$