How do I construct the incenter of a tetrahedron? Assuming that the tetrahedron in question is not regular/isoceles, of course.
Asked
Active
Viewed 2,594 times
2
-
1What do you mean by "construct" ? – Jean Marie Aug 14 '16 at 21:35
-
By incenter, do you mean the center of the unique sphere internally tangent to the four sides ? – Jean Marie Aug 14 '16 at 21:39
-
compass + straightedge, and yes, the center of the insphere. – john derrick Aug 14 '16 at 21:40
-
If you are interested by an analytical method, here is a short one (https://groups.google.com/forum/#!topic/sci.math/VsGH4BioURE). – Jean Marie Aug 14 '16 at 21:44
-
5Do you really use compass and straightedge for 3D ? – Jean Marie Aug 14 '16 at 21:44
-
1Out of curiosity, why do you assume the tetrahedron is not isosceles? – Wojowu Aug 14 '16 at 21:48
-
4How do you use compass in 3D? – Batominovski Aug 14 '16 at 22:44
2 Answers
5
The incenter is the intersection of the bisector planes of the dihedral angles formed by three tetrahedron faces which don't have a common vertex.
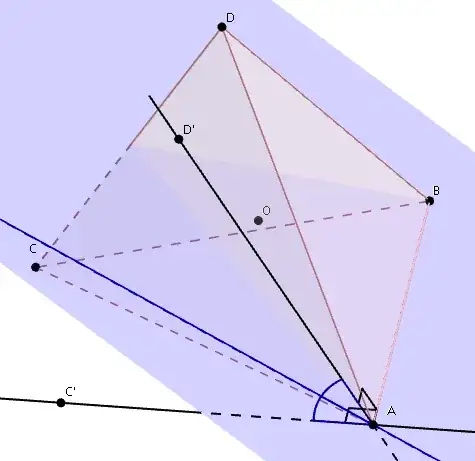
If $ABCD$ are your tetrahedron vertices, to obtain the bisector plane of planes $ABC$ and $ABD$, construct on those planes respectively lines $AC'$ and $AD'$, perpendicular to $AB$. The plane formed by the bisector of $\angle C'AD'$ with $AB$ is the bisector plane of faces $ABC$ and $ABD$. Repeat the same construction for faces $ABC$, $ACD$ and then for faces $ABC$, $DBC$.
See picture below for an example, showing perpendicular lines $AC'$ and $AD'$, their bisector (blue line) and the bisector plane of the dihedral angle formed by $ABC$ and $ABD$ (blue plane). Point $O$ is the incenter.
Intelligenti pauca
- 55,765
1
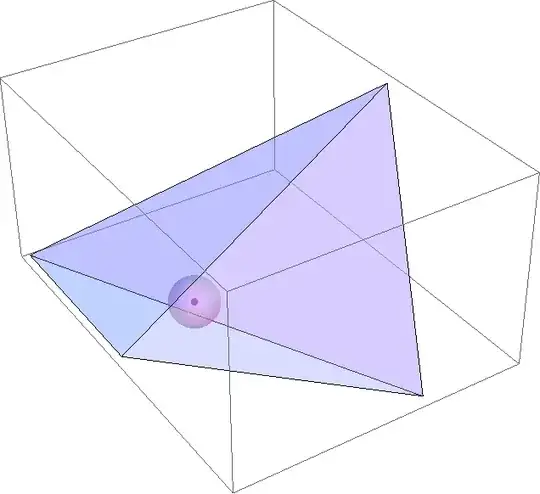
This question is computationally explored (not ruler&compass-explored) in the MathematicaSE posting, Insphere for Irregular Tetrahedron, which supplements @JeanMarie's link.
Joseph O'Rourke
- 31,079