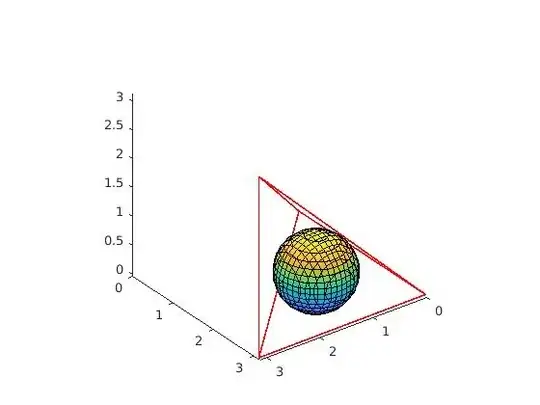
Consider the problem : "Find the maximum volume of the three dimensionnal ball inscribed to a tetraedron."
The tetraedron have the following summit (just to have a concrete case): $(0,0,0), (0,\pi,0),(\pi,0,0),(\pi,\pi,\pi)$.
Geometrically, from the optimization point of view, the problem can be formulated as
$ \begin{align} &\max_{a,b,c,r\in \mathbb{R}}\qquad r^3\\ &r-|c|<0\\ &r-|a-b|/\sqrt{2}<0\\ &r-|b-\pi|<0\\ &r-|a-c|/\sqrt{2}\\ &a-\pi<0\\ &b-\pi<0\\ &c-\pi<0\\ &a>0\\ &b>0\\ &c>0\\ &r>0\\ \end{align} $
($r$ stands for the radius of the ball of center $(a,b,c)$). The optimal volume is obtained for $r\simeq 0.65$.
Now, I have difficulty in formulating the problem with a ball of dimension $4$ in a tetraedron of dimension $4$ because I don't have the geometric point of view and I don't know how to write the constraints.