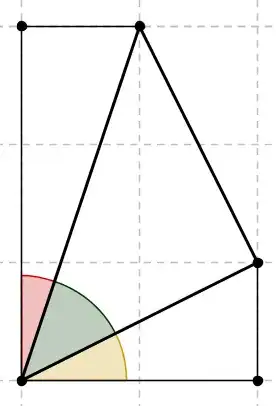
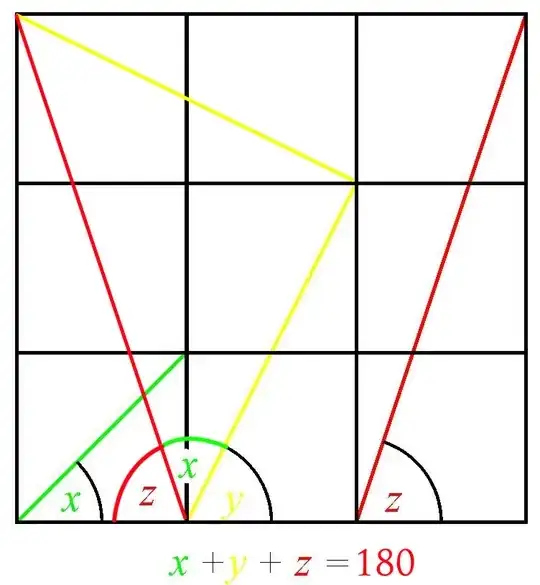
I have found the sum it's $180$ but using right triangle and sine theorem.
Asked
Active
Viewed 712 times
4
Mongol-genius
- 315
-
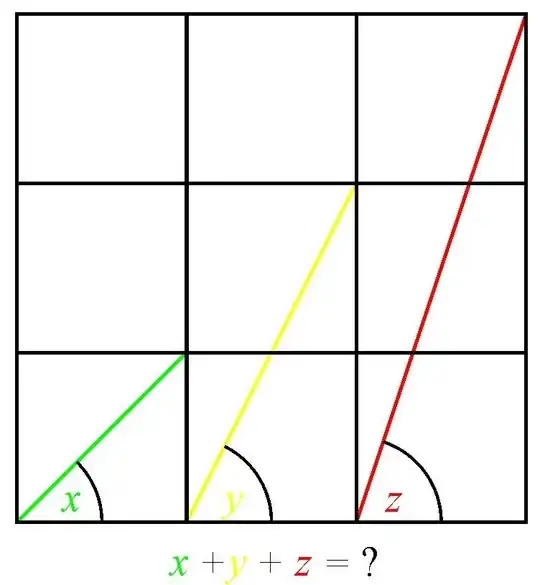
@Subhadeep Dey yes – Mongol-genius Jun 19 '16 at 12:33
-
This boils-down to the same idea as in the question "Show that the angles satisfy $x+y=z$", to which I gave this answer. The presentation may-or-may-not be distinct enough not to close this as a duplicate. (I'll leave that determination to others.) – Blue Jun 19 '16 at 14:42
-
Check out this video which solves the problem without trigonometry. – Eff Jun 19 '16 at 20:54
4 Answers
8
Just rearrange them and notice that the bold triangle is right and isosceles:
Another proof of $\arctan 1=\arctan\frac{1}{2}+\arctan\frac{1}{3}$ comes from:
$$ (3+i)(2+i) = 5+5i $$
by switching to arguments.
Jack D'Aurizio
- 361,689
-
-
@Mongol-genius: My yellow, green and red angles are the complementary angles of your yellow, green and red angles. – Jack D'Aurizio Jun 19 '16 at 12:42
-
The green angle is $45^\circ$ because the bold triangle is right and isosceles. – Jack D'Aurizio Jun 19 '16 at 12:44
-
i know it the angle $x=45^o$ but i thought if you rearrange the green yellow and red segments you have formed the triangle – Mongol-genius Jun 19 '16 at 12:48
-
@Mongol-genius: I do not understand what is the problem. You want to prove that $\arctan(1)+\arctan(2)+\arctan(3)=\pi$, and my picture above proves $\arctan 1+\arctan\frac{1}{2}+\arctan\frac{1}{3}=\frac{\pi}{2}$, that is clearly the same. – Jack D'Aurizio Jun 19 '16 at 12:50
-
if you use arctan1+arctan2+arctan3=pi you actually use the trigonometry – Mongol-genius Jun 19 '16 at 12:53
-
1@Mongol-genius: giving names to angles is using trigonometry? Well, then you want to prove that $$ yellow+green+red=\pi $$ and my proof shows that the complementary angles add to $\frac{\pi}{2}$. – Jack D'Aurizio Jun 19 '16 at 12:54
-
1
2
Consider following triangle:
As $BC = AC$ we have $\angle ABC = \angle CAB$ or $$ \pi - \gamma - \beta = \gamma - \frac{\pi}{2} + \beta \iff \gamma + \beta = \frac{3\pi}{4} $$ (here $\gamma$ is red angle from picture in question and $\beta$ is yellow one). It's obvious that green angle from question (detote it as $\alpha$) is equal to $\frac{\pi}{4}$. Thus we have $$ \alpha + \beta + \gamma = \frac{\pi}{4} + \frac{3\pi}{4} = \pi. $$
Anton Grudkin
- 3,026
1
@Jack D'Aurizio thanks for your solution and suggestions i found a little bit different solution from yours :)
Mongol-genius
- 315
0
Draw a right triangle $ABC$ with the following properties:
$A$ is at the origin.
$C$ is the right-angle vertex at $(1,1)$.
$B$ is on your "left" as seen along a line of sight from $A$ through $C$.
$BC$ is twice as long as $AC$.
Then $B$ lies at $(-1,3)$ and the straight angle at the origin, in the upper half plane, is partitioned into $\arctan(1)+\arctan(2)+\arctan(3)$.
Oscar Lanzi
- 48,208