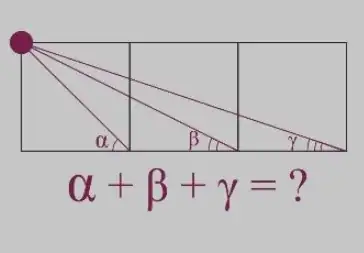0

3 square problem

In the given figure,3 squares are fitted together. Some lines are drawn. What is the value of $\alpha +\beta +\gamma$?

I just can derive alpha as 45 degree as it is an angle formed by diagonal of square. How to find the other two?

I have seen similar questions that were solved using trigonometry. I just want the process how to solve it by using only elementary geometry.

Also I saw another problem that answered its complements but I can't understand it

Jam
  • 10,632
  • 3
  • 29
  • 45
Archit Pasayat
  • 9
  • 8
  • @jam it just answers the opposite angles – Archit Pasayat Jan 22 '20 at 15:48
  • 1
    The two problems are equivalent and require similar proofs. Yours is regarding $\tan^{-1}(1)+\tan^{-1}(1/2)+\tan^{-1}(1/3)$, while the question I've linked is regarding $\tan^{-1}(1)+\tan^{-1}(2)+\tan^{-1}(3)$. Observe that $\frac{\left(\tan^{-1}\left(2\right)+\tan^{-1}\left(3\right)\right)}{3}=\tan^{-1}\left(\frac{1}{2}\right)+\tan^{-1}\left(\frac{1}{3}\right)$ and restructure one of the proofs in the linked question. – Jam Jan 22 '20 at 15:52
  • @jam I can't understand trigonometry – Archit Pasayat Jan 22 '20 at 15:53
  • I am a class 7 student – Archit Pasayat Jan 22 '20 at 15:54
  • There are proofs in question I've linked that use only elementary geometry, and rearrange the angles. I referred to the angles with trigonometry since they weren't given labels. You should be able to see how the angles can be rearranged. – Jam Jan 22 '20 at 15:55
  • Let us continue this discussion in chat. – Archit Pasayat Jan 22 '20 at 15:56
  • It may help you to cut these shapes out of a physical piece of paper and play around with them – lioness99a Jan 22 '20 at 15:56
  • See https://www.cut-the-knot.org/Curriculum/Geometry/ThreeSquares.shtml – Robert Z Jan 22 '20 at 16:02
  • I don't use the chat function. If you're not comfortable with referring to the angles with arctan, just take one of the figures from the linked question and label the angles as $\alpha,\beta,\gamma$, recall that the sum of a triangle's angles is $\pi$ radians $=180^\circ$ and go from there. – Jam Jan 22 '20 at 16:04
  • Archit and @Jam the answer by Jack is entirely in pictures and answers this question. https://math.stackexchange.com/questions/1831908/find-the-sum-of-angles-without-trigonometry/1831920#1831920 – Will Jagy Jan 22 '20 at 16:04
  • @RobertZ thanks – Archit Pasayat Jan 22 '20 at 16:08

0 Answers0