Prove that the directrix is tangent to the circles that are drawn on a focal chord of a parabola as diameter.

Question

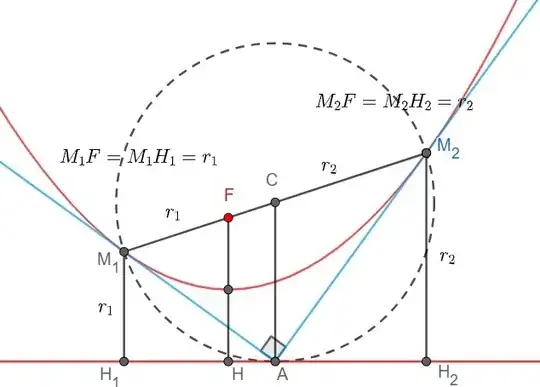
Question: Prove that the directrix is tangent to the circles that are drawn on a focal chord of a parabola as diameter.

<p>Here is a picture; <a href="https://i.sstatic.net/F8dga.png" rel="nofollow noreferrer"><img src="https://i.sstatic.net/F8dga.png" alt="enter image description here"></a></p>

---

What I have attempted;

Let the parabola be $y^2=4ax$

Hence the focus will be at $(a,0)$

Let the focal chord be $y = m(x-a) $

Subbing in $y^2=4ax$

$$y^2=4ax$$

$$ \Leftrightarrow (m(x-a))^2 = 4ax $$

$$ \Leftrightarrow m^2 (x^2-2ax+a^2) = 4ax $$

$$\Leftrightarrow m^2x^2 - 2am^2x + m^2a^2 - 4ax = 0 $$

$$ \Leftrightarrow m^2x^2 -(2am^2+4a)x + m^2a^2 = 0 $$

If $x_1$ and $x_2$ are roots then

$$ x_1 + x_2 = \frac{2am^2+4a}{m^2}$$

$$ \therefore x_1 + x_2 = 2a + \frac{4a}{m^2} $$

and $$ x_1 \cdot x_2 = \frac{m^2a^2}{m^2} $$

$$ \therefore x_1 \cdot x_2 = a^2 $$

Corresponding

$$y_1 + y_2 = m(x_1 - a + x_2 - a)$$

$$y_1 + y_2 = m(x_1 + x_2 - 2a)$$

$$y_1 + y_2 = m(2a + \frac{4a}{m^2} - 2a)$$

$$ \therefore y_1 + y_2 = \frac{4a}{m} $$

$$ y_1 \cdot y_2 = m^2(x_1-a)(x_2-a) $$

$$y_1 \cdot y_2 = m^2(x_1x_2 - a(x_1+x_2) + a^2) $$

$$ y_1 \cdot y_2 = m^2( a^2 - a^2(2 + \frac{4}{m^2}) + a^2) $$

$$ y_1 \cdot y_2 = m^2 (\frac{-4a^2}{m^2}) $$

$$ y_1 \cdot y_2 = -4a^2 $$

Now consider

$$ (x_1 - x_2)^2 = (x_1+x_2)^2 - 4x_1x_2 $$

$$ (x_1 - x_2)^2 = a^2(2 + \frac{4}{m^2})^2 - 4a^2 $$

$$ (x_1 - x_2)^2 = a^2(4+\frac{16}{m^2} + \frac{16}{m^4}) - 4a^2 $$

$$ (x_1 - x_2)^2= \frac{16a^2}{m^2} + \frac{16a^2}{m^4} $$

and

$$ (y_1 - y_2)^2 = (y_1+y_2)^2 - 4y_1y_2 $$

$$(y_1 - y_2)^2 = (\frac{4a}{m})^2 -4 \cdot -4a^2 $$

$$(y_1 - y_2)^2 = \frac{16a^2}{m^2} + 16a^2 $$

Therefore

$$ (x_1 - x_2)^2 + (y_1 - y_2)^2 = \frac{16a^2}{m^2} + \frac{16a^2}{m^4} + \frac{16a^2}{m^2} + 16a^2 $$

$$ (x_1 - x_2)^2 + (y_1 - y_2)^2 = 16a^2(\frac{1}{m^4} + \frac{2}{m^2} + 1) $$

$$ (x_1 - x_2)^2 + (y_1 - y_2)^2 = 16a^2(\frac{1}{m^2} + 1)^2 $$

Hence diameter of the circle is given as

$$ D = \sqrt{16a^2(\frac{1}{m^2} + 1)^2} $$

$$ \therefore D = 4a(\frac{1}{m^2} + 1) $$

Distance from centre of directrix is the $x$ coordinate $+a$

$$= a + \frac{2a}{m^2} + a $$

$$= 2a + \frac{2a}{m^2} $$

$$= 2a(1+\frac{1}{m^2}) $$

So distance is $2a(1+\frac{1}{m^2}) $

Also notice that the radius of the circle is given as $R = 2a(\frac{1}{m^2} + 1) $

Which equals the distance from centre to the directrix hence the directrix must be tangent to the circle.

---

Could someone please check my proof and tell me if I am correct or not (correct my working and tell me where i went wrong) or also provide me with an alternative way of approaching this question?

Answer 1

Here is a simple alternative way, fully geometrical.

Have a look at the following picture, with $M_1,M_2$ on parabola with focus $F$ and directrix $D$, $H_1, H_2, H$ the orthogonal projections on $D$ of $P_1, P_2, F$ resp.

Let $r_k:=M_kH_k=M_kF \ (k=1,2)$. Let $C$ be the midpoint of $M_1M_2$, i.e., the center of the circle with diameter $M_1M_2$. The radius of this circle is $r=\dfrac{r_1+r_2}{2}$.

In trapezoid $M_1,H_1,H_2,M_2$, consider line segment $[FH]$ joining midpoints $C$ and $H$ of line segments $M_1M_2$ and $H_1H_2$ resp. The length of $[FH]$ is the mean $\dfrac{r_1+r_2}{2}$ of the lengths $r_1$ and $r_2$ of $[M_1H_1]$ and $[M_2H_2]$ resp., i.e., the radius of the circle, as desired.

Please note the right angle in $A$ ; it refers to a classical property of focal chords such as $M_1M_2$ : the tangents to the intersections of the focal chord with the parabola 1) are orthogonal and 2) have their intersection point on the directrix.

Answer 2

An alternate way (probably shorter) would be to take two points as $(at_1^2,2at_1), (at_2^2,2at_2)$ as the ends of the focal chord.

As this chord passes through focus, we obtain $t_1t_2=-1$ Now, the equation of circle can be written in diametric form as:

$$(x-at_1^2)\left(x-\frac{a}{t_1^2}\right)+(y-2at_1)\left(y+\frac{2a}{t_1}\right)=R^2$$ Where $R$ can be written using $t_1$ and $t_2$.

Now you can differentiate this at $x=-a$ and check for the slope of the tangent.