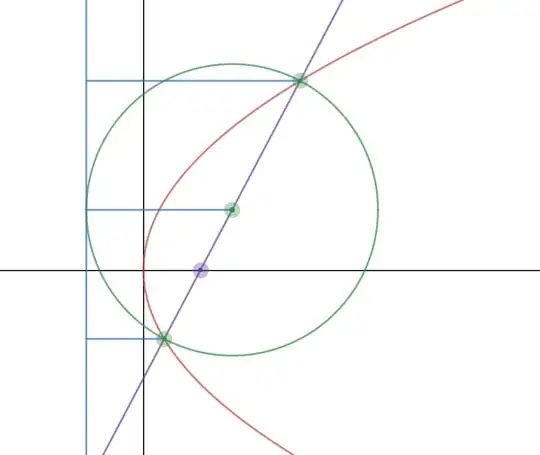
Question: Show that the circle drawn on a focal chord of a parabola $y^2=4ax$, as a diameter touches the directrix.
Let the parabola be $y^2=4ax$
Let the focal chord be $y = m(x-a) $
Subbing in $y^2=4ax$
$$y^2=4ax$$
$$ \Leftrightarrow (m(x-a))^2 = 4ax $$
$$ \Leftrightarrow m^2 (x^2-2ax+a^2) = 4ax $$
$$\Leftrightarrow m^2x^2 - 2am^2x + m^2a^2 - 4ax = 0 $$
$$ \Leftrightarrow m^2x^2 -(2am^2+4a)x + m^2a^2 = 0 $$
If $x_1$ and $x_2$ are roots then
$$ x_1 + x_2 = \frac{2am^2+4a}{m^2}$$
$$ \therefore x_1 + x_2 = 2a + \frac{4a}{m^2} $$
and $$ x_1 \cdot x_2 = \frac{m^2a^2}{m^2} $$
$$ \therefore x_1 \cdot x_2 = a^2 $$
Corresponding
$$y_1 + y_2 = m(x_1 - a + x_2 - a)$$
$$y_1 + y_2 = m(x_1 + x_2 - 2a)$$
$$y_1 + y_2 = m(2a + \frac{4a}{m^2} - 2a)$$
$$ \therefore y_1 + y_2 = \frac{4a}{m} $$
$$ y_1 \cdot y_2 = m^2(x_1-a)(x_2-a) $$
$$y_1 \cdot y_2 = m^2(x_1x_2 - a(x_1+x_2) + a^2) $$
$$ y_1 \cdot y_2 = m^2( a^2 - a^2(2 + \frac{4}{m^2}) + a^2) $$
$$ y_1 \cdot y_2 = m^2 (\frac{-4a^2}{m^2}) $$
$$ y_1 \cdot y_2 = -4a^2 $$
Now consider
$$ (x_1 - x_2)^2 = (x_1+x_2)^2 - 4x_1x_2 $$
$$ (x_1 - x_2)^2 = a^2(2 + \frac{4}{m^2})^2 - 4a^2 $$
$$ (x_1 - x_2)^2 = a^2(4+\frac{16}{m^2} + \frac{16}{m^4}) - 4a^2 $$
$$ (x_1 - x_2)^2= \frac{16a^2}{m^2} + \frac{16a^2}{m^4} $$
and
$$ (y_1 - y_2)^2 = (y_1+y_2)^2 - 4y_1y_2 $$
$$(y_1 - y_2)^2 = (\frac{4a}{m})^2 -4 \cdot -4a^2 $$
$$(y_1 - y_2)^2 = \frac{16a^2}{m^2} + 16a^2 $$
Therefore
$$ (x_1 - x_2)^2 + (y_1 - y_2)^2 = \frac{16a^2}{m^2} + \frac{16a^2}{m^4} + \frac{16a^2}{m^2} + 16a^2 $$
$$ (x_1 - x_2)^2 + (y_1 - y_2)^2 = 16a^2(\frac{1}{m^4} + \frac{2}{m^2} + 1) $$
$$ (x_1 - x_2)^2 + (y_1 - y_2)^2 = 16a^2(\frac{1}{m^2} + 1)^2 $$
Hence diameter of the circle is given as
$$ D = \sqrt{16a^2(\frac{1}{m^2} + 1)^2} $$
$$ \therefore D = 4a(\frac{1}{m^2} + 1) $$
Now I am stuck how do I show the circle touches the directrix?
I would like to know if my method is correct , and how I could continue with this.
I would also like to see alternative methods (geometrical and other algebraic)! Thank you.