What is circumradius $R$ of the great disnub dirhombidodecahedron, or Skilling's figure?

Question

The vertices of a uniform polyhedron all lie on a sphere. Out of curiosity, I looked at the circumradius $R$ of the $75$ polyhedra (non-prism) in the list (which assumed side $a=1$).

For irrational $R$, almost all were roots of quadratics, quartics, and a few sextics that can factor over a square root: $\sqrt{2},\sqrt{3},\sqrt{5},\sqrt{7},\sqrt{11}$ (and combinations thereof).

But there were two exceptions. For the snub cube and the snub icosidodecadodecahedron, it was over a cube root: $(19-3\sqrt{33})^{1/3}$ and $\big(\frac{27-3\sqrt{69}}{2}\big)^{1/3}$. Thus, their $R$ could be expressed by the tribonacci constant (root of $x^3-x^2-x-1=0$) and plastic constant (root of $x^3-x-1=0$), respectively.

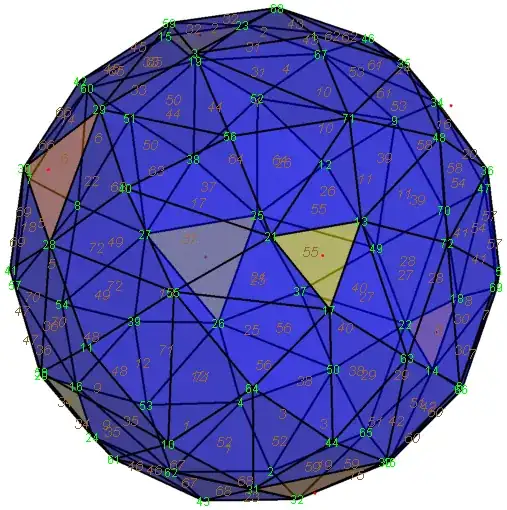
However, if the definition of a uniform polyhedron is relaxed slightly, there is a $76$th: the great disnub dirhombidodecahedron, or Skilling's figure,

$\hskip2.5in$

Q: What is the circumradius $R$ of Skilling's figure with side $a=1$?

P.S. Essentially, I'm looking for a uniform polyhedron (degenerate or not) such that the minimal polynomial of its $R$ factors over $\big(\frac{29-3\sqrt{93}}{2}\big)^{1/3}$ hence can be expressed in terms of the Narayana cow sequence constant (root of $x^3-x^2-1=0$).

Answer 1

The great disnub has identical vertices and edges as the Great dirhombicosidodecahedron, which has a circumradius of $\sqrt{2}/2$.

The Narayama cow sequence constant has a value of 0.325617..
The Pentagonal Prism Six Compound has diagonals of length 0.32492

Times 3 gets 0.97685 That's close to the lengths of the second and third longest diagonals in my caltrop. If the the 4 tetrahedral points are removed, a lot of balancing might be possible, and the second longest diagonals would be quite close to that. So, perhaps solve that figure for maximizing unit diagonals on 72 points and see if Narayana pops out. I used this shape to get excruciatingly close to a new solid of constant width, maybe this cow constant could be the key to making it work.

Answer 2

Yes I was going to say the same thing, that it has the same vertices and edges as the great dirhombicosidodecahedron, aka Miller's Monster, and thus has the same radius, $\frac{\sqrt 2}{2}$. I'll just add a quick explanation of why, since there's a simple way to see it. Both polyhedra have square faces that pass through the centre of the model, so the circumradius of the polyhedron is just half the diagonal of a square with edge length 1, hence $\frac{\sqrt 2}{2}$.

Answer 3

Here are some wheels of similar triangles where the sides are powers of the square root of Narayana Cow Sequence constant. I should look through my canonical polyhedra list. As a side note, $t^6-4t^4-t^3+4t^2+2t-1$ works perfectly for the Snub Dodecahedron.

Answer 4

(This is an addendum to E. Pegg's answer and too long for a comment.)

If there is a degenerate uniform polyhedron with unit side and a circumradius $R$ that involves the Narayana cow sequence constant, then the discriminant of $R$'s minimal polynomial should be integrally divisible by $d=31$.

The assumption is as follows: Given fundamental discriminant $d$, there are exactly two imaginary quadratic fields with class number $h(-d)=3$ such that the Weber class polynomial $W$ has degree $3$. Furthermore, $W$ has unit coefficients. These are $\mathbb{Q}(\sqrt{-23})$ and $\mathbb{Q}(\sqrt{-31})$,

$$x^3-x-1 = 0,\quad x = P = \tfrac{\zeta_{48}\eta(\tau)}{\sqrt{2}\,\eta(2\tau)} = 1.3247\dots,\quad\tau = \tfrac{1+\sqrt{-23}}{2}$$

$$x^3-x^2-1 = 0,\quad x = N = \tfrac{\zeta_{48}\eta(\tau)}{\sqrt{2}\,\eta(2\tau)} = 1.4655\dots,\quad\tau = \tfrac{1+\sqrt{-31}}{2}$$

where $\zeta_{48}$ is the $48$th root of unity $e^{2\pi i/48}$, and $\eta(\tau)$ is the Dedekind eta function. Furthermore, though $\mathbb{Q}(\sqrt{-11})$ has $h(-d)=1$, we also have,

$$-x^3-x^2-x+1 = 0,\quad x = \frac{1}{T} = \tfrac{\zeta_{48}\eta(\tau)}{\eta(2\tau)}-1 = 0.5436\dots,\quad\tau = \tfrac{1+\sqrt{-11}}{2}$$

$P,N,T$ have other similarities. All are Pisot numbers, all are limiting ratios of well-known sequences, all appear in pi formulas, etc, etc. Since there is a geometric solid for $P$ and $T$, there might be a solid (degenerate, semi-regular, etc) for $N$ as well.