This question has been edited.
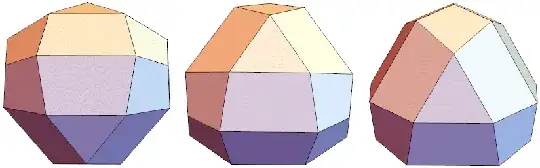
The regular tetrahedron is a caltrop. When it lands on a face, one vertex points straight up, ready to jab the foot of anyone stepping on it.
Define a caltrop as a polyhedron with the same number of vertices and faces such that each vertex is at distance 1 from most of the corners of the opposing face. Are there any other caltrops besides the tetrahedron?
Use these 5 values in the list of vertices that follow.
$\text{C0}=0.056285130364630088035020091792834$
$\text{C1}=0.180220007048851841582537343751297$
$\text{C2}=0.309443563867344767680227839435148$
$\text{C3}=0.348675924605445651138054435209609$
$\text{C4}=0.466391197450500551933366795454853$
verts =(
(C1,C1,C4),(C1,-C1,-C4),(-C1,-C1,C4),(-C1,C1,-C4),(C4,C1,C1),(C4,-C1,-C1),
(-C4,-C1,C1),(-C4,C1,-C1),(C1,C4,C1),(C1,-C4,-C1),(-C1,-C4,C1),(-C1,C4,-C1),(C3,-C0,C3),(C3,C0,-C3),(-C3,C0,C3),(-C3,-C0,-C3),(C3,-C3,C0),(C3,C3,-C0),
(-C3,C3,C0),(-C3,-C3,-C0),(C0,-C3,C3),(C0,C3,-C3),(-C0,C3,C3),(-C0,-C3,-C3),(C2,C2,C2),(C2,-C2,-C2),(-C2,-C2,C2),(-C2,C2,-C2));
The resulting polyhedron has the following appearance, arranged so that each of the three types of faces is on the bottom:
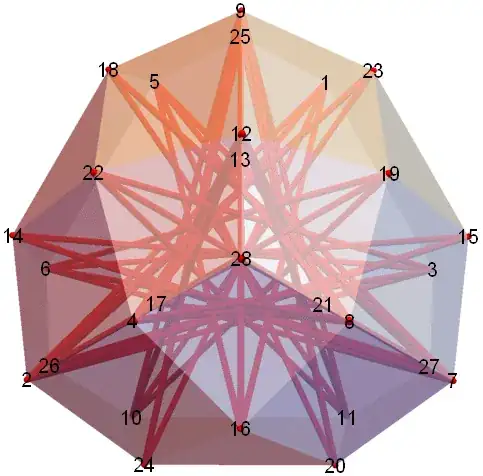
Here's a transparent picture showing the 48 unit diagonals.
Diagonals $(13-16, 14-15, 17-19, 18-20, 21-22, 23-24)$ have a length of about $~0.98620444$. I'm not sure of the maximum length, and don't have exact values for coordinates.
That's one more caltrop. Are there any others?
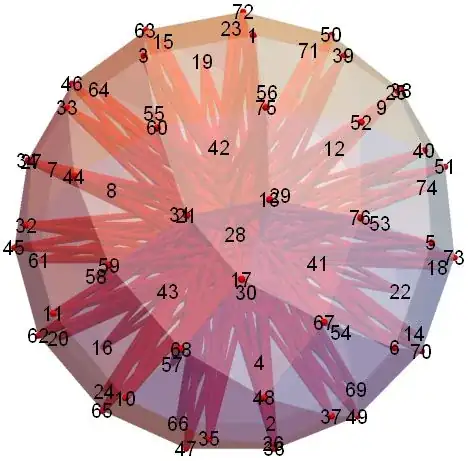
Rahul pointed out that some faces of my initial caltrop weren't exactly planar. This new version fixes that error, but I had to sacrifice 6 unit diagonals. A stronger caltrop would have each vertex at distance 1 from all corners of an opposing face, instead of most corners.