2

When I read my textbooks or even type "what is a tangent?" on google, I have always got an answer similar to these lines: "A straight line or plane that touches a curve or curved surface at a point, but if extended does not cross it at that point." Now when I am thinking about graph of $\sin x$ or $\cos x$, it is very hard for me to believe this definition because if we draw a line touching any point on such curves then either it will cut at some point or touch at (infinitely) many points. So therefore it is very hard for me to believe this concept (or definitions).

Please correct me if I am wrong at any point suggest a better definition in good mathematical framework.

Image in support of question

litmus
  • 681
Tesla
  • 179
  • 1
    it just means it doesn't cross at the point at which it is tangent. It may or may not cross at other points. – Set Dec 28 '15 at 09:50
  • @thoth No in few texts it is clearly written that it neither touches curve at another point nor cuts . please post link in support . – Tesla Dec 28 '15 at 09:53
  • well, it must be called a tangent to a curve at a point. The tangent,the curve and the point all are needed for the definition. So it doesn't matter what the tangent does at some other point. You are perhaps too young, as you read more you 'll automatically realize it. Its better to think how one would have phrased the definition to keep it clear and unambigous – Ricky Dec 28 '15 at 09:54
  • I need a detailed answer developed on mathematical foundations ( axioms & analysis ) – Tesla Dec 28 '15 at 09:56
  • @Ricky please refer a text . – Tesla Dec 28 '15 at 09:57
  • 1
    I don't know what texts you're reading but the definition you give is non-standard as far as I'm concerned. – Set Dec 28 '15 at 10:00
  • @Ricky ya I am young but not too young to learn this concept . I have recently started bartle & sherbert ( real analysis ) . – Tesla Dec 28 '15 at 10:01
  • after all if tangency required that it not intersect at any point then all you'd be left with are the convex/concave functions. In fact you can't even restrict non-intersection to a local neighborhood, e.g. $y=x^3$ at $(0,0)$. – Set Dec 28 '15 at 10:03
  • @Thoth please type what is tangent on google . i have copied & pasted it from google . but i am asking question after searching a suitable definition in many texts ( college level ) . I also came across few curves where a line was touching only at a single point but it was not called tanget . – Tesla Dec 28 '15 at 10:04
  • @Thoth thanx bro – Tesla Dec 28 '15 at 10:04
  • I would suggest just taking a look at the wikipedia article on the concept of a tangent – Set Dec 28 '15 at 10:05
  • Consult any text related to differential geometry. If you can understand Cauchy's definition of limits ($\epsilon$ & $\delta$ stuff), then there is nothing more i can offer you. Good luck with your real analysis. Have patience and things will sort themselves out – Ricky Dec 28 '15 at 10:08
  • @Ricky thanks for wishes . – Tesla Dec 28 '15 at 10:11
  • The (entirely standard) definition in A Course in Pure Mathematics: https://books.google.co.uk/books?id=oEp0kpPpLB4C&pg=PA210 . – Chappers Dec 28 '15 at 10:21
  • Some interesting debate is here also:https://ca.answers.yahoo.com/question/index?qid=20101115202240AAIivpB – NoChance Dec 28 '15 at 11:30
  • A good description of the problem and its solution is here: Book:Calculus: Early Transcendental Functions - Page 116 - Section: 3.1:https://books.google.ca/books?id=zUfAAgAAQBAJ&pg=PA116&dq=definition+%22tangent+to+a+curve%22++points&hl=en&sa=X&ved=0ahUKEwiY-Mi7vP7JAhWDuBQKHR2KAbEQ6AEINjAD#v=onepage&q=definition%20%22tangent%20to%20a%20curve%22%20%20points&f=false – NoChance Dec 28 '15 at 11:52
  • @litmus thanks for edit – Tesla Dec 28 '15 at 12:40
  • Related: Can someone provide the formal definition of the tangent line to a curve? – Andrew D. Hwang Dec 28 '15 at 12:51
  • On a tangent (as it were), the Cambridge third edition (1921) of Hardy's A Course of Pure Mathematics is available (typeset in LaTeX) from Project Gutenberg, and in HTML5 from the Sayahna Foundation. – Andrew D. Hwang Dec 28 '15 at 12:53
  • @ArshbrahmDwivedi, sure thing, hope the answer helped as well. – litmus Dec 28 '15 at 12:54

2 Answers2

4

If the mathematical definition on Wikipedia feel too abstract, then maybe this animated image can help. It helped me understand what a tangent is, maybe it can help you.

In the animation (link above), pay no attention to the mathematical formulas nor any of the number vaules. Focus on the line that is gliding along the curve. Remember that it, i.e. the tangent, is a tool to show you how much the function/curve is "rising" or "falling" at that specific point. When you look at the animation notice how the tangent-line shifts color between,

-$ \bf \color{green} {Green} $: for the parts of the function when its Y-value is increasing, i.e. climbing,

-$ \bf Black$: for the parts of the function when its Y-value is constant, i.e. terrace/ local maximum or minimum point,

-$ \bf \color{red} {Red}$: for the parts of the function when its Y-value is decreasing.

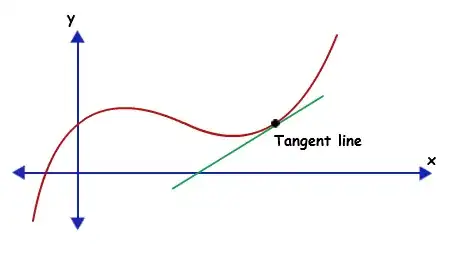
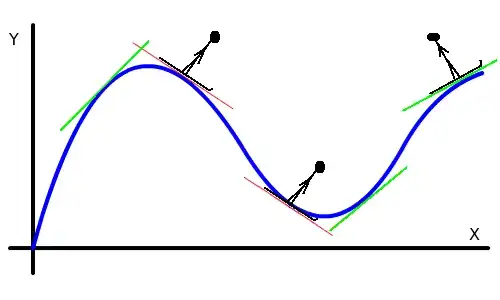
Notice also that the tangent does not have to extend infinity long from its point. In the picture below you will see a (green) tangent-line which can be made to extend further or be shortened, it doesn't matter, since its main function is to show you the angle of the slope at that specific X-value.enter image description here

Finally here is how my teacher introduced me to tangent lines: "Think of the tangent line as the skis belonging to a person skiing on a curvy mountain (which is your function). The center of the skis are always parallel with the curve, and the skier is always standing perpendicular to the skis." See image below:

enter image description here

litmus
  • 681
  • This is a good intuitive meaning of a tangent line for a first encounter, but it's not really suitable as a definition. For example, it's not helpful for determining existence or uniqueness of a tangent line. Visual inspection cannot, in practice, tell you whether a specific line is or is not tangent to a curve, because the curve could have a "kink" too small to see at a particular scale. What happens at $x = 0$ for the graph $y = |x|$? The graph $y = \sqrt{10^{-100} + x^{2}}$? (Not down-voting, but I suspect the OP already understands the "skis" picture. :) – Andrew D. Hwang Dec 28 '15 at 13:11
  • 2
    I see your point, but wikipedia can help with the definition. And since OP was talking about the tangent line possibly 'touching' infinitely many points in a $\cos x$ curve I thought it best to show how the tangent is a 'local' measurement. – litmus Dec 28 '15 at 15:31
1

HINTS:

A geometrical picture. Take curve like a U curve but facing down. Take a straight line rigid stick and place it on the curve to cut it at two points, which are the two roots. Now displace line parallel to itself so the roots approach each other until they become a single point. The roots are coincident, now you have a point of tangency between curve and the moving line. If you continue the motion further the roots are imaginary, no real roots, no cutting. Most the math of tangency is a symbolic representation of this simple situation. For a coincident root the discriminant of the constitutive quadratic equation has a zero discriminant.

Choice of different points at tangency result in different slopes to the curve.

Narasimham
  • 42,260