2

The most common answer to this question "What is tangent to any curve?" is as follows:

"Tangent to a plane curve at a given point is the straight line that "just touches" the curve at that point. "

But this definition have two problems.

First is what do you mean by "just touches"? How can I know if a line "just touches" a curve or not?

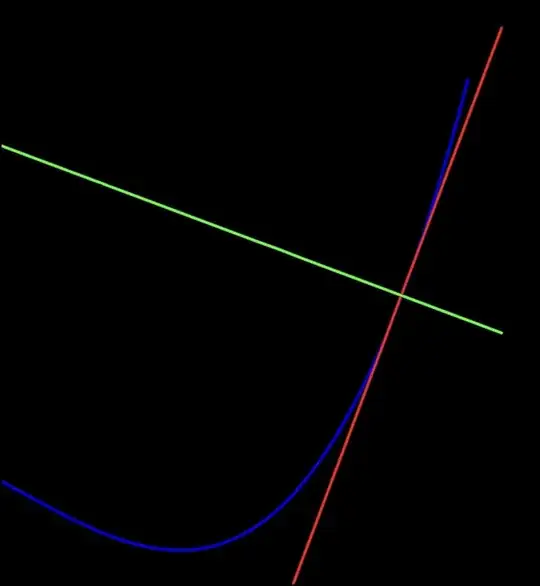
For example: How do you know that the red line in the following image "just touches" the curve while green line doesn't?

image

Second problem is that this definition doesn't generalize to the "straight-line curve" .

A tangent to a straight line is the straight line itself. But this can't be possible under the "just touches" definition. (This is just what I think, if you think my reasoning is incorrect then please correct me.)

So what is tangent to any curve? And also if my objections are correct then why is this definition so famous?

Jean Marie
  • 88,997
  • 1
    limit of secants? – J. W. Tanner Jul 19 '20 at 02:34
  • There are probably many ways to answer this, depending on what the exact question is. Do you know one-variable calculus? – pancini Jul 19 '20 at 02:46
  • 3
    It's the line that best approximates the curve at that point. – saulspatz Jul 19 '20 at 02:48
  • @ElliotG I don't know calculus. Actually this question came to me when I started to learn differentiation! –  Jul 19 '20 at 02:54
  • 3
    This is not a definition, but rather the intuition behind the true definition. – Ningxin Jul 19 '20 at 03:04
  • This topic has been discussed at length on this website. Please do your research before asking. – K.defaoite Jul 19 '20 at 03:06
  • @K.defaoite I had searched on the site: https://stackexchange.com/search?q=what+is+tangent+to+any+curve%3F+ The most close question was this https://math.stackexchange.com/questions/1591370/what-is-tangent-to-a-curve-or-function but none of the answer were rigours and satisfied me. –  Jul 19 '20 at 04:02
  • 1
    As @QiyuWen notes, that's not a definition, but an intuition. (Also, it's the etymology of the term "tangent" itself, which comes from the Latin tangere, "to touch".) My intuitionistic answer to the question "What is a tangent line?" is this: "The tangent at a point on a curve is the line that the curve looks like when you zoom in really-really-really close to that point." In your example, the green line is clearly not such a line; on the other hand, the red line actually appears to obscure the curve near the point in question, even at "low zoom", making it a good candidate. – Blue Jul 19 '20 at 04:19
  • 2
    As for why the (not-a-)definition is "so famous" ... Likely, it stems from the idea that tangents were (and still tend to be) first introduced in the context of circles, where "just touches" quite accurately and unambiguously captures the sense of things. It also conveys the right idea in the context of, say, conic sections. It's the natural descriptor to use for curves in general. However, with generality comes ambiguity and the potential for confusion (as in your objections), which is why we cannot (and do not) rely on "just touches" as a definition. – Blue Jul 19 '20 at 04:38
  • Come to think of it ... In the context of conic sections, "just touching" is more-or-less definitional for ellipses and hyperbolas, since a line can meet such a curve in one, two, or no points. But parabolas already highlight a need for caution, since there are two ways for a line to meet a parabola at a single point. Nowadays, we have the formality of Calculus (as well as a "projective" understanding of conics) to distinguish the tangent and non-tangent lines for the parabola. I'm kinda curious about how ancient mathematicians handled this nuance in the earliest treatises on conics. – Blue Jul 19 '20 at 05:22

3 Answers3

1

intuitively; In the plane a line $ l $ is tangent to a curve $ c $ at point $ A $ if it is the only line that satisfies:

  1. there is a region $ R $ of the plane such that $ l \cap c = \{A\} $ or $ A \in l \cap c $

  2. $ l $ divides $ R $ into two regions $ R_1 $ and $ R_2 $ such that $ R_1 \cap c = \emptyset $ or $ R_2 \cap c = \emptyset $

Fractal Admirer
  • 470
AsdrubalBeltran
  • 4,222
0

I think that the "just touches" means that "it doesn't go through". Maybe by looking to the contrapositive (the one I just mentioned) you will be "happier". And by the "just touches" in the sense that "it doesn't go through", a straight line tangent to another "just touches it". But yes, it is not the most rigorous approach and definitely not the one I would use, but it can be useful for the abstraction of this concept, if it satisfies you.

Fractal Admirer
  • 470
  • @it isn't satisfactory. Go to this site: https://www.desmos.com/calculator/4pf1dxxzq2 Move the slider (below $a=-5.8$) and you will find that the tangent at lot many of point is crossing the curve and not just touching it. –  Jan 20 '21 at 07:07
  • I agree, it isn't satisfactory. But this approach is more applicable for people that aren't going to study rigorous mathematics, in my opinion. I wouldn't teach my students this way though... – Fractal Admirer Jan 20 '21 at 23:45
0
  • A tangent line to $f(x)$ must intersect $f(x)$ at a point $(a,f(a))$.
  • The slope of the tangent line must be equal to the instantaneous slope of $f(x)$ at $x=a$.

This doesn't restrict the tangent line from intersecting $f(x)$ at any point outside of the local tangency region, nor does it prevent linear graphs from having tangent lines congruent to them.

VV_721
  • 799