Envelope of Projectile Trajectories

Question

For a given launch velocity $v$ and launch angle $\theta$, the trajectory of a projectile may be described by the standard formula $$y=x\tan\theta-\frac {gx^2}{2v^2}\sec^2\theta$$

For different values of $\theta$ what is the envelope of the different trajectories? Is it a parabola itself?

The standard solution to this "envelope of safety" problem is to state the formula as a quadratic in $\tan\theta$ and set the discriminant to zero. The resulting relationship between $x,y$ is the envelope.

This question is posted to see if there are other approaches to the solution.

---

Edit 1

Thanks for the nice solutions from Jack and Blue, received so far. From the solution of the envelope it can be worked out that the envelope itself corresponds to the right half of the trajectory of a projectile launched at $(-\frac{v^2}{g^2},0)$ at a launch angle $\alpha=\frac{\pi}4$ and a launch velocity $V=v\sqrt2$. This means that both vertical and horizontal components of the launch velociy are equal to $v$. It would be interesting to see if these conclusions can be inferred from the problem itself by inspection and without first solving it. If so, then this would form another solution.

---

See also this other question posted subsequently.

Answer 1

Yes it is. To find the envelope, we just have to find the intersections between two trajectories associated to two slightly different angles. If we solve $$ x\tan\theta -\frac{gx^2}{2v^2}\sec^2(\theta) = x\tan(\theta+\varepsilon) -\frac{gx^2}{2v^2}\sec^2(\theta+\varepsilon) $$ we get $x=0$ or $$ x=\frac{2v^2}{g}\cdot\frac{\tan(\theta)-\tan(\theta+\varepsilon)}{\sec^2(\theta)-\sec^2(\theta+\varepsilon)}$$ and by letting $\varepsilon\to 0$ we get $x=\frac{v^2}{g}\cot(\theta)$, from which $y=\frac{v^2}{2g}\left(2-\frac{1}{\sin^2(\theta)}\right) $.

It follows that the equation of the envelope is given by: $$ y = \frac{v^2}{2g}\left(1-\left(\frac{gx}{v^2}\right)^2\right)=\frac{v^2}{2g}-\frac{g}{2 v^2}\,x^2$$ that clearly is a parabola with vertex in $\left(0,\frac{v^2}{2g}\right)$ through the points $\left(\pm\frac{v^2}{g} ,0\right)$.

We may notice that the envelope and the trajectory with $\theta=\frac{\pi}{4}$ are homothetic, and the dilation ratio is just $2$. The vertices of the trajectories lie on an ellipse that is tangent to the envelope parabola, with centre at $\left(0,\frac{v^2}{4g}\right)$, a vertex in the origin and a vertex at $\left(\frac{v^2}{2g},\frac{v^2}{4g}\right)$.

Answer 2

@Jack provides a very nice and intuitive derivation of the envelope as the points of intersection of infinitely-close members of the curve family. The Wikipedia "Envelope" entry provides this less-illuminating abstraction:

The envelope of the family [of curves parameterized by $t$ is] the set of points for which $$F(t, x, y) = \frac{\partial F}{\partial t}(t,x,y) = 0 \tag{$\star$}$$ for some value of $t$ [...].

In $(\star)$, $F$ is the function that, when set equal to $0$, defines each curve in the family. For the question at hand, we have (with parameter $\theta$ instead of $t$) $$F(\theta,x,y) = -y + x\tan\theta -\frac{g x^2}{2v^2}\sec^2\theta \tag{1}$$ Therefore, differentiating with respect to $\theta$ gives $$\frac{\partial F}{\partial \theta}(\theta,x,y) =x\sec^2\theta -\frac{g x^2}{2v^2}\cdot 2 \sec^2\theta\tan\theta = \frac{x\sec^2\theta}{v^2} ( v^2 - g x \tan\theta) \tag{2}$$ Solving $\partial F/\partial \theta = 0$ for $\theta$ (noting that $\sec\theta$ never vanishes) gives $$\tan\theta = \frac{v^2}{g x} \qquad\text{so that}\qquad \sec^2\theta = 1 + \tan^2\theta = \frac{g^2 x^2 + v^4}{g^2 x^2}$$

Substituting into $(1)$, and setting $F=0$, we have

$$y = x\;\frac{v^2}{gx} - \frac{g x^2}{2 v^2}\;\frac{g^2 x^2 + v^4}{g^2 x^2} = \frac{v^2}{2g} - \frac{g x^2}{2v^2} = \frac{v^4-g^2x^2}{2gv^2}$$

which agrees with Jack's answer.

Answer 3

Another way to think about this is as follows:

Assume a point $(x,y)$ in the plane. For a given velocity $v$, if we get a real value of $θ$, then the point lies inside the envelope. In general, there are two values of $θ$ for a given point because the equation of trajectory is a quadratic in $\tan θ$ (you can break the $\sec^{2} θ$ as $1+ \tan^{2} θ$).

If the discriminant $D$ of the quadratic is greater than zero, then the point lies inside the envelope. If it is equal to zero, then it lies on the envelope. If $D$ is less than $0$, then it lies outside the envelope.

So, $D=0$ of the equation of trajectory gives us the equation of envelope

I hope you would like this analogy.

Answer 4

Here's another approach. Not as elegant as Jack's though. Perhaps similar to Blue's. (Edit: Revised slightly to use substitution of $H=v^2/2g$ instead of $\lambda=g/v^2$ for more convenient reference, per solution by Narasimham)

This approach maximises the value of $y$ for any given value of $x$.

For a given value of $x$, say $x=k$, $$\begin{align} y&=kT-\frac {k^2}{4H}(1+T^2)\qquad\text{where $T=\tan\theta, H=\frac {v^2}{2g}$}\\ \frac{dy}{dT}&=k-\frac {k^2}{4H}\cdot 2T=0\qquad\text{when $T=\frac {2H}k$}\\ \text{At $T=\frac {2H}k$}:\qquad\qquad y&=k\cdot\frac{2H}k-\frac{k^2} {4H}\left(1+\frac {4H^2}{k^2}\right) \color{lightgrey}{=2H-\frac {k^2}{4H}-H}\\ &=H-\frac {k^2}{4H} \end{align}$$

Hence the equation of the envelope is $$y=\frac {v^2}{2g}-\frac {gx^2}{2v^2}\quad\blacksquare$$

Answer 5

Although there are several very nice solutions provided above, here is another approach. No calculus is needed.

Consider a projectile launched with angle $\theta$ with relation to an inclined plane with tilt angle $\varphi$. The initial speed is $v_0$. We want to know at what distance from the launch point the projectile will hit the inclined plane. We use a Cartesian coordinate system rotated by the angle $\varphi$ (see figure 1). The trajectory is given by \begin{aligned} x'(t) &=v_{0x'}t+\frac{g_{x'}t^2}2,\\ y'(t) &= v_{0y'}t+\frac{g_{y'}t^2}2, \end{aligned} where $x'$ and $y'$ indicate the coordinates of the projectile in the rotated coordinate frame. Furthermore, we have $v_{0x'}=v_0\cos\theta$, $v_{0y'}=v_0\sin\theta$, $g_{x'}= -g\sin\varphi$ and $g_{y'}=-g\cos\varphi$. At the point where the projectile hits the inclined plane $y'=0$. Hence, we obtain that the time span for the collision is $t_{hit}=-2v_{0y'}/g_{y'}$. Replacing this time, we find \begin{aligned} x'_{hit} &=-2\frac{v_{0x'}v_{0y'}}{g_{y'}}+2\frac{g_{x'}v^2_{0y'}}{g^2_{y'}}\\ &=\frac{v_0^2}{g\cos^2\varphi}\left[\cos\varphi\sin(2\theta)-\sin\varphi(1-\cos(2\theta))\right]\\ &=\frac{v_0^2}{g\cos^2\varphi}\left[\sin(2\theta+\varphi)-\sin\varphi\right] \leq\frac{v_0^2}{g\cos^2\varphi}\left(1-\sin\varphi\right)=\frac{v_0^2}{g(1+\sin\varphi)}. \end{aligned} If we now turn to polar coordinates, the envelope of the projectile trajectories is given by $$ r(\varphi)=\frac{v_0^2}{g(1+\sin\varphi)},\qquad(1) $$ with $0\leq\varphi\leq\pi$. See in figure 2 that this curve is the envelope.

Projectile trajectory hitting an inclined plane

Envelope given by equation (1)

Answer 6

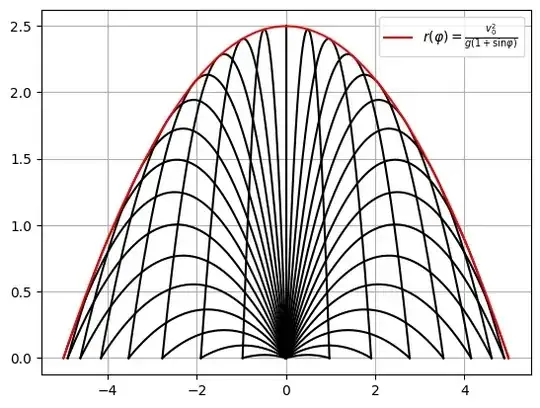
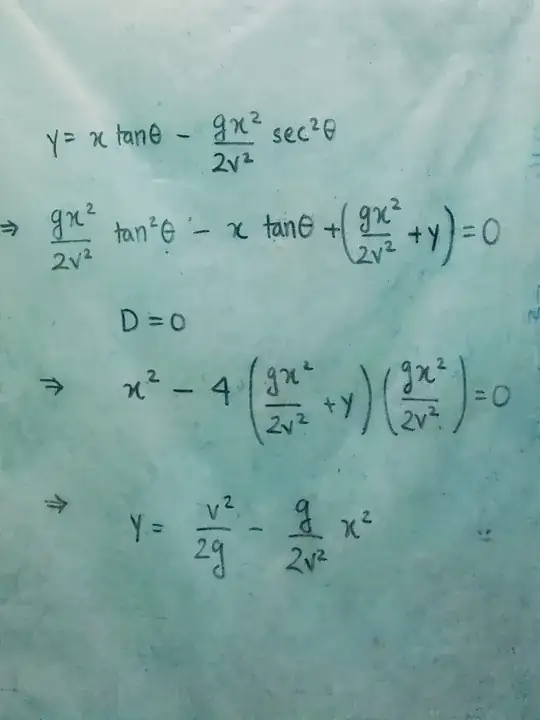I shall outline the method how we get the parabola. Usual notation

$$ \ddot y = -g, \quad \dot y = - g t + v \sin \theta , \quad y =- g t^2/2 + v t \sin \theta\, +0 \tag {1} $$ $$\ddot x = 0, \quad \dot x = v \cos \theta = \text{const}, \quad x = v t \cos \theta +0 \tag{2}.$$

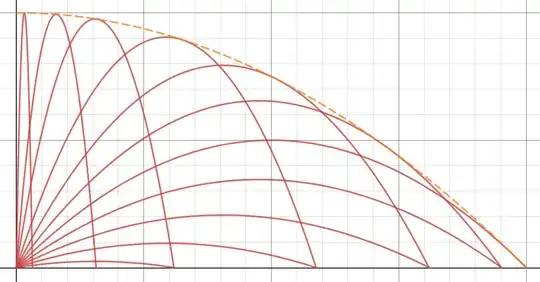
Eliminating time $t$ between $(1)$, $(2)$ you got this parabola equation already.

Let $\tan \alpha = T$; parabola equation in other words

$$ y = x T - g/2 \cdot (x/ v \cos\theta)^2 = x T - ( g x^2/2 v^2) ( 1+T^2) .\tag{3} $$

Differentiate partially with respect to $T$ and simplify, $T = v^2 / gx .\tag{4}$

Eliminate $T$ between $(3)$ and $(4)$

$$ y = v^2/2g - g x^2 /(2 v^2) = H - x^2/(4H) \tag{5}, $$

same as what was obtained before by Jack and Blue.

If you denote height reached by projectile on vertical firing $ H = v^2/(2g) \tag{6} $ you would notice that the envelope is profiled exactly as a parabolic mirror with focus at gun delivery point, focal length is exactly H. Vertical force of gravity is acting like light :)..

The above procedure method is indicated by Blue in Wiki, is referred to as C-discriminant method to obtain envelopes and singular solutions.

Like what you said in your edit and I about mirror, they are ploys for remembering curves using similarities..

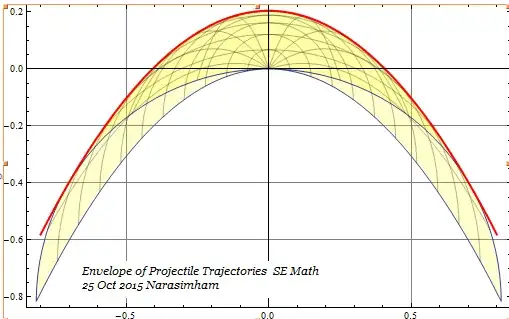
For the image I took values of $ g=9.8 \, \mathrm{m/s^2}, \quad v = 2 \, \mathrm{m/s} $

The partial differentiation way and elimination is the right way to look at, perhaps not as what you said (standard solution.. way).

EDIT2:

The answer to your second question, i.e., to determine if it is going to be a parabola envelope without going through all of analysis... I can only reply with extended C-discriminant, strengthening the same result by another path.

$p$ discriminant method is also relevant, but I defer it, but best is to refer to differential calculus books of authors e.g., A.R. Forsythe.

I shall expand on the C-discriminant, wherein a two parameter system of equations variation of any of the two parameters leads to the same parabola envelope. This is in reply to your question , Why do you also plot partial concentric circles?

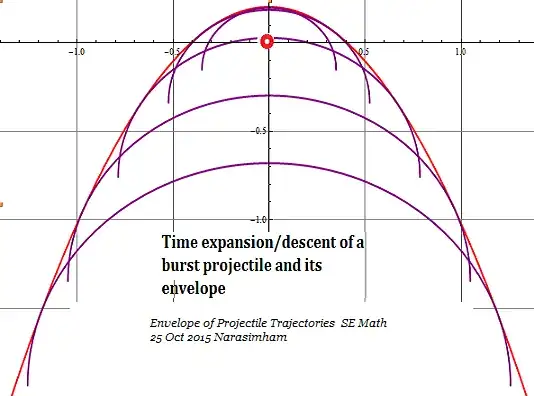
Well, they are circles alright, but not concentric circles. They expand and come down slowly with time. What you can see as plotted are the peripheries traced out descending with time .

But first quickly watch some fireworks to see what I am discussing about:

Expanding & Descending Fire-Works Circle Periphery

It is common experience to see fire ball bright splinters expanding to bigger circles as the entire cluster comes down slowly with time. The periphery of burst splinters is a portion of a circle whose radius increases during slow descent. The center of circle is always descending by gravity.

The two parameters are $ \theta, t $ angle of elevation at first burst or fire, and time $t$.

By C-discriminant method the parabola envelope is the eliminant of either $\theta$ variable or

$$ F(x,y,\theta) =0 ,\, F_{\theta } (x,y,\theta) =0 \tag{6} $$

or $t$ time variable.

$$ F(x,y, t) =0 ,\, F_{t } (x,y, t) =0. \tag{7} $$

The first one is already discussed, the second one is expanding/descending fireworks circles as already stated.

In the latter case working is:

$$ x = v t \cos \theta , \quad y = v t \sin \theta - g t^2/2 \tag{8}$$

$$ \left(\frac{x}{vt}\right)^2 + \left(\frac{y+ gt^2/2}{vt}\right) ^2 = 1 \tag{9}$$

$$ x^2 + ( y + g t^2/2)^2 = v^2t^2. \tag{10} $$

which is a Circle.

To find its envelope, as before partially differentiate with respect to time $t$ and cancel $ 2t$ on either side of equation , bring $ v^2/g$ to right side :

$$ y + gt^2/2 = v^2/g \tag {11} $$

$$ x^2 + (v^2/g)^2 = 2 v^2/g * ( v^2/g-y) \tag {12} $$

$$ x^2 + ( 2 H)^2 += 4 H ( v^2/g -y )\tag{13} $$

$$ x^2 = 4 H ( H-y) \tag{14} $$

which is the same parabola envelope obtained earlier with $\theta $ as parameter. End points $ ( x=0, \quad y=H ; x= 2 H, \quad y= 0 ) $

Although circle end traces are visible in a fireworks display it needs imagination as before with variable gun barrel angle to see that each circle is tangent to a fixed envelope. Hope you enjoyed it.

Answer 7

Here is a solution that does not require considering angles; my end goal is to say something like "{something} is degree 2 in {something else} so it has to be a degree 2 curve", but this solution doesn't quite get there yet:

The space of physical configurations that can arise from launching a projectile from the origin is 3 dimensional, because it can be parameterized as $(v_x,v_y,t)$ where $v_x,v_y$ are the $x$- and $y$- velocities at the start and $t$ is how much time has passed. So the initial velocity is $v_x^2+v_y^2$.

This space can also be parameterized as $(x,y,t)$, where $(x,y)$ is the final position and $t$ is how much time has passed; then (choosing coordinates so that gravity is 1), $x=v_xt, y=v_yt-\frac{t^2}{2}$.

So, $$v_x=\frac{x}{t}\quad v_y=\frac{y}{t}+\frac{t}{2}$$ and if our initial velocity bound is $E$ then we want to find for which $(x,y)$ it holds that $$\min v_x^2+v_y^2=\min \frac{x^2}{t^2}+\frac{y^2}{t^2}+y+\frac{t^2}{4}\le E.$$

In general, for $A,B>0$, $\min_{h}\frac{A}{h}+Bh=2\sqrt{AB}$ achieved when $h$ is chosen so the two addends are equal (e.g., by AM-GM).

Taking $h=t^2, A=x^2+y^2, B=\frac{1}{4}$, gives $$\min \frac{x^2}{t^2}+\frac{y^2}{t^2}+y+\frac{t^2}{4}=2\sqrt{\frac{x^2+y^2}{4}}+y=\sqrt{x^2+y^2}+y$$ and the inequality $$\sqrt{x^2+y^2}+y\le E$$ is equivalent to $$\sqrt{x^2+y^2}\le E-y$$ which bounds a parabola with focus $(0,0)$ and directrix $y=E$.

(That the focus is $(0,0)$ has the interpretation that the set of points that can be reached by a projectile starting at the origin with kinetic energy $\frac{E}{2}$ is the same as the set of points that can be reached by a gravity-less projectile starting at the origin with kinetic energy $\frac{1}{2}$ that gets vaporized if it ever touches a laser beam that starts at $y=E$ and decreases at a rate of 1.

Everything in this problem is dilation invariant, so it suffices to show the claim for one value of $E$.)