2

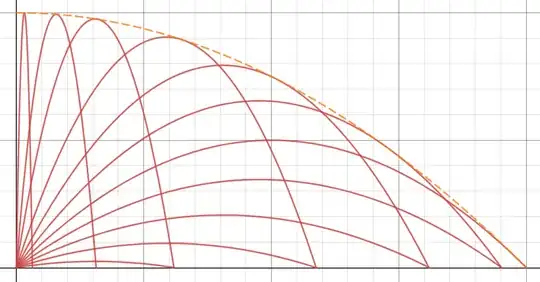
enter image description here

Consider a projectile launched from the origin at velocity $v$ and angle $\theta$. From this other question we see several approaches to arrive at the equation for the envelope of different trajectories with varying $\theta$.

We know from standard projectile formulas that
(i) at $\theta=\frac \pi 4$, the projectile reaches maximum horizontal range of $\frac {v^2}g$, and
(ii) at $\theta=\frac \pi2$, the projectile is launched vertically and reaches a maximum height of $\frac {v^2}{2g}$.

Hence the $x$-axis intercept of the envelope is $\dfrac {v^2}g$ and the $y$-axis intercept is $\dfrac{v^2}{2g}$.

Can it be concluded, without first working out its equation, that the envelope is a parabola symmetrical about the $y$-axis?

If so, then, together with the axes intercepts deduced above, the formula for the envelope can be derived directly.

NB - if we know that the envelope is a parabola symmetrical about the $y$-axis, with $x$- and $y$- intercepts $\dfrac {v^2}g$ and $\dfrac {v^2}{2g}$ respectively, then the formula for the envelope is $$\frac {x^2}{\left(\dfrac {v^2}{g}\right)^2}+\frac y{\left(\dfrac {v^2}{2g}\right)}=1$$ which reduces to the standard result for the envelope $$y=\frac {v^2}{2g}-\frac {g}{2v^2}x^2$$

Note: Just found a usefeul reference here, with an alternative approach.

Hypergeometricx
  • 23,235
  • Indeed, the envelope I compute is $x^2+2y\frac{v^2}g=\frac{v^4}{g^2}$; however, I computed the trajectories first. I don't see a way yet to do this without first computing the trajectories. – robjohn Sep 28 '18 at 19:30

1 Answers1

2

I put together an argument that I think relies only on true facts and avoids actually computing either the envelope's equation or the equation of any trajectory. I suspect that the proofs of the facts used in this argument require (at least in some cases) more sophistication than the calculation using the discriminant (mentioned in the linked question), and altogether this argument may take more effort than simply working out the equation. But here it is:

Select a line through the origin at an arbitrary angle $\alpha$ counterclockwise from the positive $x$ axis, with $0 < \alpha < \frac\pi2.$ The farthest point on that line that can be hit by the projectile launched to the right of vertical is achieved when the initial velocity angle of the projectile is $\frac12\left(\frac\pi2 - \alpha\right)$ clockwise from vertical. That is, in order to maximize the distance reached on a sloped line, we bisect the angle between the sloped line and the vertical line through the launch point.

Moreover, if we take the velocity with which the projectile arrives at $P$ and consider all possible trajectories outward from $P$ at that velocity with an initial angle to the left of vertical, the farthest point on the line that we can reach is the origin, reached by retracing the original projectile's path from the origin to $P.$ Therefore the tangent to the projectile's parabolic path at $P$ (which is also the tangent to the envelope at $P$) bisects the angle between the sloped line and the vertical line through $P.$ The tangent line is therefore sloped downward to the right at an angle $\frac12\left(\frac\pi2 - \alpha\right)$ from horizontal.

The reflection of the ray from the origin to $P$ off the tangent line at $P$ is a vertical line.

This holds for every sloped line through the origin: wherever that line meets the envelope, the line is reflected by the tangent to the envelope into a vertical line.

The only continuous curves that have this property (all lines outward from the origin are reflected by the tangent of the curve into vertical lines) are parabolas with focus at the origin, symmetric across the $y$ axis. You only need to examine one point on the envelope (such as the highest point reached by shooting straight up) in order to determine which parabola is the envelope.

David K
  • 108,155