Envelope curve of parabola

Question

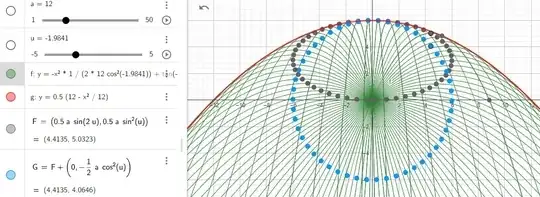
About a year ago, I came across a really cool property of the envelope curve of a parabola that I couldn't prove. I'm posting it now for help: If we have a straight line and a circle that belong to one plane, then the enveloping curve of the parabola whose focus is a moving point on the circumference of the circle and whose guide is that straight line forms two parabolas that can be drawn with the four information: the perpendicular from the center of the circle on the line is the axis of symmetry of the two parabolas, the distance between the guides of the two parabolas is equal to the length of The diameter of the circle, the center of the circle is a common focus of the two parabolas, the straight line is midway between the two guides.

If you start from a circle that does not share the line at any point, the segment will leave traces of two parabolas inside each other, as shown in the picture

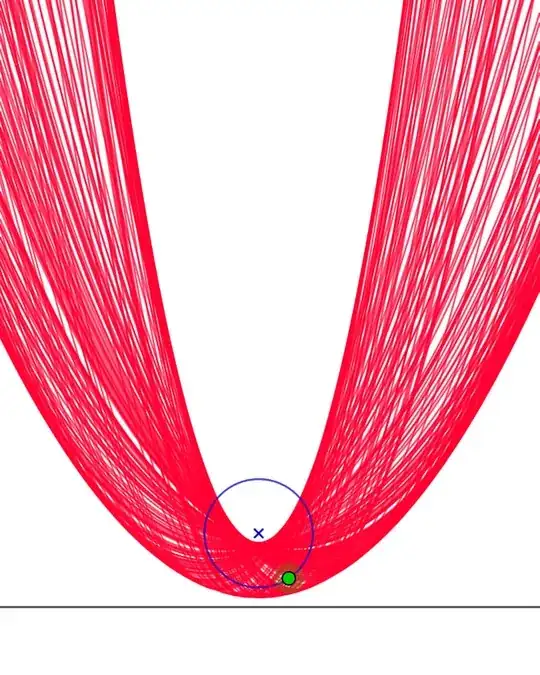
But if you start with a circle cutting the straight line, leave the traces of two intersecting parabolas at two points on this straight line.

But if a circle starts touching the straight line, then the traces of one parabola touching the straight line will be left

I was hoping to prove it myself, but unfortunately my level of proof does not allow me. Please do a complete proof that discusses the three cases, please, and thank you.

Also, is this feature previously discovered or is it new, please attach a reference if it was previously discovered

Answer 1

A purely geometrical proof can be given. Consider indeed a circle (centre $C$ and radius $R$) and a line $b=HK$. Taken any point $F$ on the circle, we can draw the parabola (blue in the figure) with focus $F$ and directrix $b$.

Line $CF$ intersects that parabola at two points $A$, $B$, labeled so that $C$ is between $A$ and $F$. If $H$ is the projection of $A$ on the directrix $b$, we have by definition $FA=AH$. But then we also have $CA=AD$, where $D$ is the projection of $A$ on line $r$, parallel to $b$ and at a distance $R$ from it on the same side as $C$, because $CA=FA-R$ and $AD=AH-R$. Hence $A$ also belongs to the parabola (red in the figure) with focus $C$ and directrix $r$. Moreover, both parabolas have the same tangent line at $A$ (the bisector of angle $\angle FAH$), hence they are tangent at $A$.

In a similar way we can show that point $B$ also belongs to the parabola (green in the figure) with focus $C$ and directrix $g$ parallel to $b$ and at a distance $R$ from it, on the opposite side of $C$. As before, green and blue parabolas are tangent at $B$.

Hence, all parabolas with focus $F$ are tangent to the red and blue parabolas, which are then (by definition) their envelope.

The above proof works if the distance between $C$ and $b$ is greater than $R$. The other cases can be treated in an analogous way.

Answer 2

This issue, in the case of parabolas, is in fact classical ; it is the set of shooting parabolas (see the answers to this question) : a cannon placed at the origin, inclined at angle $\alpha$ sends a projectile with speed $v_0$ ; this projectile has a parabolic trajectory with equation :

$$y=- \frac{x^2}{2a \cos^2 \alpha}+(\tan \alpha) x \ \ \text{with} \ \ a=\frac{v_0^2}{g}\tag{1}$$

The set of these parabolas has an envelope which is the so-called "parabola of safety" with equation

$$y=\frac12 \left(a-\frac{x^2}{a}\right)\tag{2}$$

An ill-known result (see here for example) is that the set of foci of these parabolas is a circle with parametric equations :

$$\frac12 a( \sin(2\alpha), \cos(2\alpha))\tag{3}$$

which is a way to (partially) answer your question.

Moreover the set of their apexes is an ellipse (see figure).

Remark : Parametric equations (3) have been obtained by using the following results (see here) : a parabola with equation $y=ax^2+bx+c$ has its apex in $\left(\frac{-1}{2a},\frac{-\Delta}{4a}, \right)$ and its focus in $\left(\frac{-1}{2a},\frac{1-\Delta}{4a}, \right)$ (its directrix having equation $y=\frac{-1-\Delta}{4a}$) with $\Delta = b^2-4ac$, of course.