Let $A$ be a $3\times 3$ real matrix with all $0\leq a_{ij}\leq 1$. Show that $\det A \leq 2$.
So the hint my classmates give was to assume all $a_{ij}=\{1,0\}$. Why is that? Why does considering these binary matrices improve the estimate on determinant? (making $\det$ closer to 2). then I think the rest follows using the permutation formula for determinant. (or the dumbest way, is to compute all the matrices with full rank that are binary).
Taking the determinant of a matrix yields a continuous map $$\det:\ \operatorname{Mat}(3\times3,\Bbb{R})\ \longrightarrow\ \Bbb{R}:\ A\ \longmapsto\ \det(A),$$ where $\operatorname{Mat}(3\times3,\Bbb{R})$ is homeomorphic to $\Bbb{R}^9$. Your question concerns the subspace $$C:=\{A=(a_{ij})_{i,j}\in\operatorname{Mat}(3\times3,\Bbb{R})\mid\ (\forall i,j\in\{1,2,3\})(a_{ij}\in[0,1])\}\subset\operatorname{Mat}(3\times3,\Bbb{R}),$$ which is compact and connected. Because $\det$ is continuous it follows that $\det[C]=[a,b]$ for some $a,b\in\Bbb{R}$, and in particular $\det$ takes on a maximum on $C$.
Let $A=(a_{ij})_{i,j}\in C$ a matrix for which $\det(A)$ is maximal, and suppose $a_{11}\notin\{0,1\}$. Then $a_{11}\in(0,1)$, and we denote by $A_0$ and $A_1$ the matrices obtained from $A$ by setting $a_{11}=0$ and $a_{11}=1$, respectively. Let $A_{ij}$ denote the minor of $A$ obtained by removing the $i$-th row and the $j$-th column of $A$. Then the cofactor expansion of $\det(A)$ with respect to the first row is $$\det(A)=a_{11}\det(A_{11})-a_{12}\det(A_{12})+a_{13}\det(A_{13}).$$ If $\det(A_{11})>0$ then from $1>a_{ij}$ we find \begin{eqnarray*} \det(A_1)&=&1\cdot\det(A_{11})-a_{12}\det(A_{12})+a_{13}\det(A_{13})\\ &>&a_{11}\det(A_{11})-a_{12}\det(A_{12})+a_{13}\det(A_{13})\\ &=&\det(A), \end{eqnarray*} contradicting the maximality of $\det(A)$. Similarly, if $\det(A_{11})<0$ then from $0<a_{11}$ we find \begin{eqnarray*} \det(A_0)&=&0\cdot\det(A_{11})-a_{12}\det(A_{12})+a_{13}\det(A_{13})\\ &>&a_{11}\det(A_{11})-a_{12}\det(A_{12})+a_{13}\det(A_{13})\\ &=&\det(A), \end{eqnarray*} again contradicting the maximality of $\det(A)$. It follows that $\det(A_{11})=0$ and hence $\det(A)=\det(A_0)=\det(A_1)$, which shows that $\det$ also takes on its maximum at $A_0$ and $A_1$.
Repeating this process for all $i,j\in\{1,2,3\}$ shows that $\det$ takes on its maximum at a matrix $A=(a_{ij})_{i,j}$ with $a_{ij}\in\{0,1\}$ for all $i,j\in\{1,2,3\}$.
One may also try pure geometrical constructions similar to Kepler's work on Platonic solids in his Mysterium Cosmographicum.
The constraint on the matrix elements means that the matrix columns are vectors inside the positive unit cube with one vertex being in the origin. The determinant of $A$ is the (signed) triple vector product which is related to the volume of the parallelepiped spanned by the columns. Since the volume of the tetrahedron is just one sixth of that of the parallelepiped, we can state our problem equivalently as
find the largest tetrahedron (by volume) that fits inside the unit cube.
The picture looks like in this question. To solve this problem we first take a step aside and find out the largest tetrahedron that fits inside a sphere of a fixed radius.
Proposition: The largest tetrahedron that fits inside a given sphere is a regular inscribed tetrahedron.
Proof: Clearly, the largest tetrahedron must be inscribed, i.e. to have all vertices on the sphere, otherwise one can move the vertex which is assumed to be strictly inside in such a way that the altitude to the base increases to get contradiction with maximality of the volume.
Now take any three vertices on the sphere, say $A$, $B$, $C$, and assume them to be fixed. They define the plane that cuts the sphere along a circle that is circumscribed around the triangle ABC. The most distant point on the sphere from this plane is on the line that is orthogonal to the circle plane and goes through its center. The fourth vertex, say $D$, must be in this position (the largest of the two possibilities), otherwise the altitude, i.e. the distance from $D$ to $ABC$ and, hence, the volume can be increased by moving $D$ to this position. But if the projection of $D$ onto the plane $ABC$ is the circumcenter of $ABC$ then $D$ is equidistant from $A$, $B$ and $C$.
Repeating this argument to all other triples, we get that the tetrahedron is regular.$\qquad \blacksquare$
Now we can return to the cube. The cube can be inscribed in a sphere. Any tetrahedron in the cube is a tetrahedron in the sphere, and we know that the largest inside the sphere is the regular inscribed tetrahedron. One such tetrahedron looks like this one
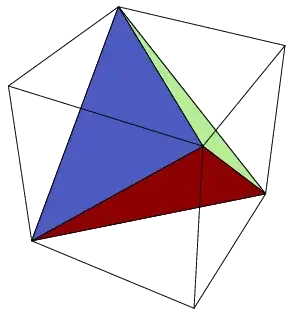
It is one of two that build Kepler's stella octangula. It is a regular inscribed in the sphere tetrahedron. All others inside the cube will either not be inscribed in the sphere or not be regular, hence, must have smaller volumes.
It gives a nice geometrical explanation why the extremal columns should have $\{0,1\}$-elements simply because they belong to the unit cube vertices. The problem of maximizing the determinant for binary matrices is known as Hadamard's problem.
