An ellipse is usually defined as the locus of points so that sum of the distances to the two foci is constant. But what are curves called which are defined as the locus of points so that the sum of the distances to three foci is constant? Trilipse? And what about $n$ foci? $n$-lipse? How do these curves look like? Is there any literature about them?
Asked
Active
Viewed 6,697 times
40
J. M. ain't a mathematician
- 76,540
asmaier
- 2,763
-
2A link about your question. http://en.wikipedia.org/wiki/N-ellipse – Mathlover Mar 25 '12 at 19:54
-
@dtldarek Unsure how you are relating the affine base to the metric condition (sum of distances from the selected points is constant)?? – Mark Bennet Mar 25 '12 at 19:59
-
@MarkBennet Yeah, you are right, what I said is completely unrelated. – dtldarek Mar 25 '12 at 20:19
-
This link is also interesting: https://en.wikipedia.org/wiki/Generalized_conic#Multifocal_oval_curves – asmaier Mar 20 '16 at 21:24
1 Answers
32
These are called $k$-ellipses.
Yes, there is a literature.
Here is one 2007 reference, which can
lead you to others: "Semidefinite Representation of the $k$-Ellipse,"
arXiv:math/0702005v1:
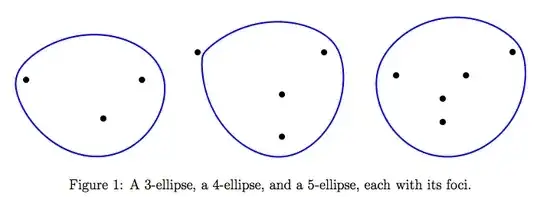
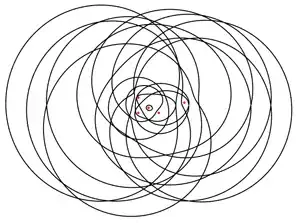
Caveat emptor: The Zariski closure of the 5-ellipse is an algebraic curve
of degree 32(!). See their Fig.5:
Joseph O'Rourke
- 31,079
-
4This French page deals with a bunch of generalizations of Cayley ovals, which are the loci of a point whose distance from a given set of foci satisfy an algebraic relation. In general, if $n$ is the number of foci, then the degree of the underlying algebraic curve is $2^n$. – J. M. ain't a mathematician Mar 28 '12 at 20:31