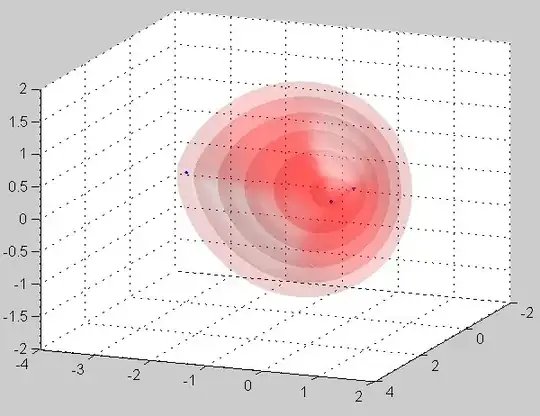
I'm trying to think of a 3D analogue to the ellipse, but not the ellipsoid.
A circle is constructed with a piece of string anchored at the radius. So the distance from center to the curve is always the same.
An ellipse is constructed with a piece of string ending at two foci. The sum of the two lines is always the same.
For 3D, I can think of 3 ways:
Three points define a plane. These are our 3 foci. Make lines from each of them that meet at some point on the curve of the shape. But the 3 lines must always sum to the same number. (I'm pretty sure this is not and ellipsoid, but possibly, if 2 foci coincide, it would be an ellipsoid?)
Three points define a plane. These are our 3 foci. Make lines from each of them that meet at some point on the curve of the shape. This also defines a tetrahedon. The surface area of the tetrahedron must be constant.
Same as above, except we want the volume of the tetrahedron to be constant.
What do those shapes look like? Maybe someone knows how to program a 3D model, or graph it somehow? If so please post pictures.