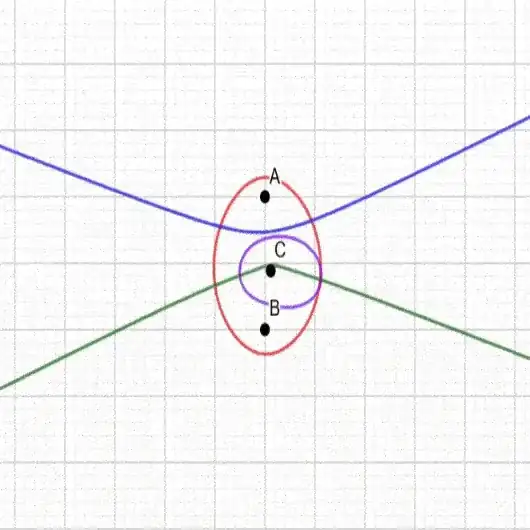
I recently learned about k-ellipses (see this other question) and I wondered if there was such a thing about k-hyperbolae. I have seen the Wikipedia article on 'Generalized Conics', but I'm not able to discern their application to hyperbolae.
The question I have is what would hyperbolae with multiple focal points look like (if they even exist)? A picture of a 3-ellipse is given on Wikipedia's N-ellipse page. I can imagine something akin to a 3-hyperbola being hyperbolas between any two of the vertices, but I'm not sure if that follows the generalized conic description.
An additional question is if they do exist, is there a literature on them?