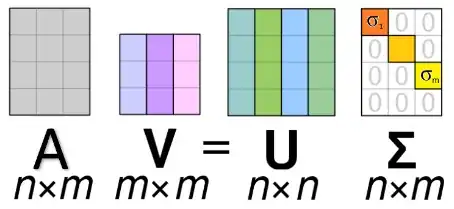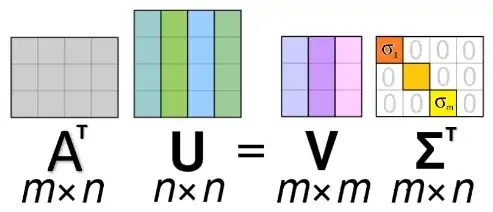46

As a part of an exercise I have to prove the following:

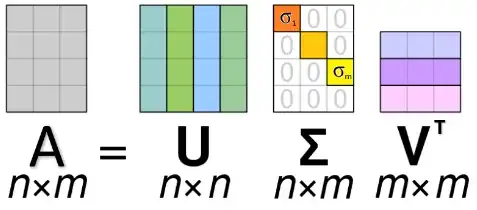
Let $A$ be an $(n \times m)$ matrix. Let $A^T$ be the transposed matrix of $A$. Then $AA^T$ is an $(n \times n)$ matrix and $A^TA$ is an $(m \times m)$ matrix. $AA^T$ then has a total of $n$ eigenvalues and $A^TA$ has a total of $m$ eigenvalues.

What I need to prove is the following:

$AA^T$ has an eigenvalue $\mu \not = 0$ $\Longleftrightarrow$ $A^TA$ has an eigenvalue $\mu \not = 0$

In other words, they have the same non-zero eigenvalues, and if one has more eigenvalues than the other, then these are all equal to $0$.

How can I prove this?

Thanks and regards.

5 Answers5

87

Let $\lambda$ be an eigenvalue of $A^TA$, i.e. $$A^T A x = \lambda x$$ for some $x \neq 0$. We can multiply $A$ from the left and get $$A A^T (Ax) = \lambda (Ax).$$

What can you conclude from this?

Huy
  • 6,867
  • 5
    what happens if $x \in ker(A)?$ not that it can happen. – abel Dec 31 '14 at 23:47
  • 6
    @abel If $Ax=0$, then $\lambda x=0$ and $\lambda=0$. So, if we assume $\lambda\ne0$… – egreg Jan 01 '15 at 00:18
  • 2
    @egreg, i know; but that needed to be part of the answer. egret you must like linear. this is the second time we meet, the other one at eigenvalues 1, -1, and 4. – abel Jan 01 '15 at 00:21
  • 7
    Further, same proof holds for any $A$ and $B$ as mentioned by @abel. Given $ABx = \lambda x$, multiplying by $B$, yields $BABx = B \lambda x$ $\Rightarrow$ $BA(Bx) = \lambda (Bx)$. So, $AB$ and $BA$ share the eigenvalues. – kamalbanga Sep 05 '18 at 12:03
  • 7
    Answers should not pose further questions without answering them themselves. This site is not for teaching the OP, it is for reference. – crow Sep 13 '22 at 02:58
24

in fact, nonzero eigenvalues $AB$ and $BA$ are the same for any rectangular matrices $A$ and $B$. this follows from the fact that $trace((AB)^k) = trace((BA)^k)$ and the coefficients of the characteristic polynomials of a square matrix $A$ are a function of $trace(A^k).$

abel
  • 29,612
  • So we can we say that the non-zero eigenvalues of $AB$ and $BA$ also have the same algrebraic multiplicity. – Curtis74 Nov 23 '19 at 15:00
9

One proof that comes to mind is to use Sylvester's determinant theorem.

In particular: $$ \mu \neq 0 \text{ is an eigenvalue of }A^TA \implies\\ \det(A^TA - \mu I) = 0 \implies\\ \det(I + (-1/\mu)A^TA) = 0 \implies\\ \det(I + A(-1/\mu)A^T) = 0 \implies\\ \det(AA^T - \mu I) = 0 \implies\\ \mu \neq 0 \text{ is an eigenvalue of }AA^T $$

Ben Grossmann
  • 234,171
  • 12
  • 184
  • 355
9

SVD is definitely an overkill, but maybe it would be helpful to you (as it is for me) to draw the matrices that the decomposition gives us:

SVD

Recall that:

  • The columns of $V$ (right-singular vectors) are eigenvectors of $A^TA$.
  • The columns of $U$ (left-singular vectors) are eigenvectors of $AA^T$.
  • $V^T=V^{-1}$ and $U^T=U^{-1}$.

With some simple operations you can get:

derived from SVD 1

And also:

derived from SVD 2

Write down both of these equations, but for the $i^\text{th}$ column.
From there, the solution is not far.

Oren Milman
  • 521
  • 6
  • 11
0

following the way as

https://math.stackexchange.com/a/1087065/1421431 shows I'll provide more details into the eigenvector, and personally I don't think that the SVD or any other advanced techniques are necessary, as they're too complicated.

It's obvious that if $$ ABx = \lambda x $$ then $$ B\cdot (ABx) = (BA)\cdot (Bx) = \lambda (Bx) $$ As eigenvector cannot be $0$, it's fine that if $Bx\neq 0$, then $\lambda$ is also eigenvalue for $BA$. For $A^T Ax = \lambda x$, it's evident that $Ax = 0 \rightarrow \lambda = 0$, then I'll prove that $\lambda = 0 \rightarrow Ax = 0$: $$ A^T Ax = 0 \\ x^T A^T Ax = 0 \\ (Ax)^T (Ax) = 0 \\ Ax = 0 $$ So once $\lambda \neq 0$, we can prove that it's also eigenvalue for $AA^T$, and the same for $AA^T$.

lingheng
  • 1