improving Neural network regression model

Question

I have the following toy data (which closely mimicks my original larger data used for the project):

x = np.array([ 0.        ,  0.1010101 ,  0.2020202 ,  0.3030303 ,  0.4040404 ,
        0.50505051,  0.60606061,  0.70707071,  0.80808081,  0.90909091,
        1.01010101,  1.11111111,  1.21212121,  1.31313131,  1.41414141,
        1.51515152,  1.61616162,  1.71717172,  1.81818182,  1.91919192,
        2.02020202,  2.12121212,  2.22222222,  2.32323232,  2.42424242,
        2.52525253,  2.62626263,  2.72727273,  2.82828283,  2.92929293,
        3.03030303,  3.13131313,  3.23232323,  3.33333333,  3.43434343,
        3.53535354,  3.63636364,  3.73737374,  3.83838384,  3.93939394,
        4.04040404,  4.14141414,  4.24242424,  4.34343434,  4.44444444,
        4.54545455,  4.64646465,  4.74747475,  4.84848485,  4.94949495,
        5.05050505,  5.15151515,  5.25252525,  5.35353535,  5.45454545,
        5.55555556,  5.65656566,  5.75757576,  5.85858586,  5.95959596,
        6.06060606,  6.16161616,  6.26262626,  6.36363636,  6.46464646,
        6.56565657,  6.66666667,  6.76767677,  6.86868687,  6.96969697,
        7.07070707,  7.17171717,  7.27272727,  7.37373737,  7.47474747,
        7.57575758,  7.67676768,  7.77777778,  7.87878788,  7.97979798,
        8.08080808,  8.18181818,  8.28282828,  8.38383838,  8.48484848,
        8.58585859,  8.68686869,  8.78787879,  8.88888889,  8.98989899,
        9.09090909,  9.19191919,  9.29292929,  9.39393939,  9.49494949,
        9.5959596 ,  9.6969697 ,  9.7979798 ,  9.8989899 , 10.        ])
y = np.array([-0.80373298,  0.76935298, -0.14159923,  1.29519353,  0.3094064 ,
        0.66238427,  0.42343774,  0.77283061,  1.47505766,  0.45931619,
        1.41141125,  1.62579566,  1.28840108,  1.34285815,  0.9329334 ,
        1.329214  ,  1.5139391 ,  1.21117778,  0.54639438,  0.51462165,
        2.77181805,  1.13110837,  1.86706418,  1.95244603,  1.40661855,
        1.30664676,  1.79014375,  1.39412399,  1.17882416,  1.06187797,
        1.89504248,  1.50652787,  1.64920352,  2.69228877,  2.24660016,
        1.8767469 ,  2.22418453,  1.63944449,  1.81288111,  1.59961924,
        1.7354012 ,  1.65975252,  2.04371439,  2.51920563,  2.3971049 ,
        1.74297775,  2.22420045,  1.29922847,  1.78963033,  2.76862922,
        2.59913081,  2.5868994 ,  0.95132831,  2.33654116,  2.14236444,
        2.56886641,  2.41801508,  2.03847576,  1.76058536,  1.47914731,
        3.22155981,  2.77761667,  2.43482125,  2.87060182,  2.71857598,
        2.39742888,  2.55224796,  2.03309053,  2.85056195,  3.01513978,
        3.1316874 ,  2.14246426,  1.88901478,  2.30135553,  2.90525156,
        3.08009528,  2.0941706 ,  3.05404934,  3.59780609,  2.32416305,
        3.04954219,  1.36782575,  3.16888341,  2.26659839,  2.14637558,
        3.26594114,  3.47156645,  3.27828348,  3.48980836,  2.66734284,
        2.69708374,  2.90246668,  2.48449401,  3.13271428,  3.08989781,
        3.05270477,  3.96243953,  3.28104845,  2.46014121,  3.95762993])

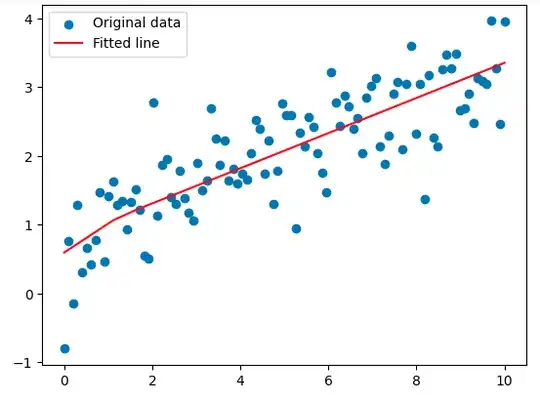
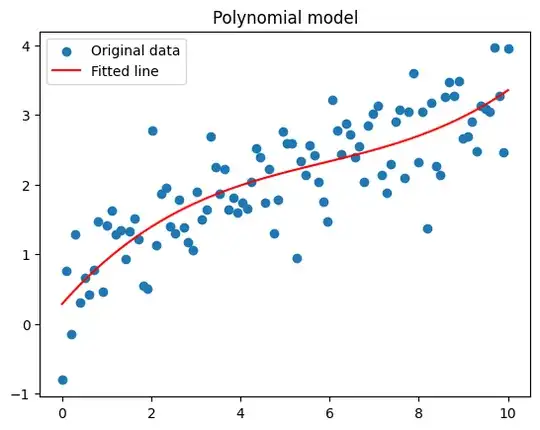
my goal is to do a regression/fit to the data and obtain a good model which can reciprocate this data pattern.For this I used initially, simple polynomial regression, then neural network, with a single layer, then with 2 layers, however in all cases, I am unhappy at how it fails to grasp the pattern at the low x values where the data dips suddenly (along Y axis).

from tensorflow import keras
import numpy as np
import matplotlib.pyplot as plt
# Reshape x to be a 2D array of size (N, 1)
x = x_data
y = y_data
x = x.reshape(-1, 1)
Define the model
model = keras.models.Sequential([
    keras.layers.Dense(10, input_dim=1, activation='relu'),  # input layer and hidden layer with 10 neurons
    keras.layers.Dense(1)                                    # output layer with 1 neuron
])
Compile the model
model.compile(loss='mean_squared_error', optimizer='adam')
Train the model
model.fit(x, y, epochs=500, verbose=0)
Make predictions with the model
y_pred = model.predict(x)
Plot the original data and the model's predictions
plt.scatter(x, y, label='Original data')
plt.plot(x, y_pred, color='red', label='Fitted line')
plt.legend()
plt.show()

Second try :

import numpy as np
import matplotlib.pyplot as plt
from tensorflow import keras
x = x_data
y = y_data
Preprocess data
x = x.reshape(-1,1)  # Needs to be reshaped for Keras
y = y.reshape(-1,1)
Building the model
model = keras.models.Sequential([
    keras.layers.Dense(64, activation='relu', input_shape=x.shape[1:]),
    keras.layers.Dropout(0.2),
    keras.layers.Dense(64, activation='relu'),
    keras.layers.Dropout(0.2),
    keras.layers.Dense(1)
])
Compile the model
model.compile(optimizer='adam', loss='mse')
Train the model
history = model.fit(x, y, epochs=50, verbose=0)
Make predictions with the model
y_pred = model.predict(x)
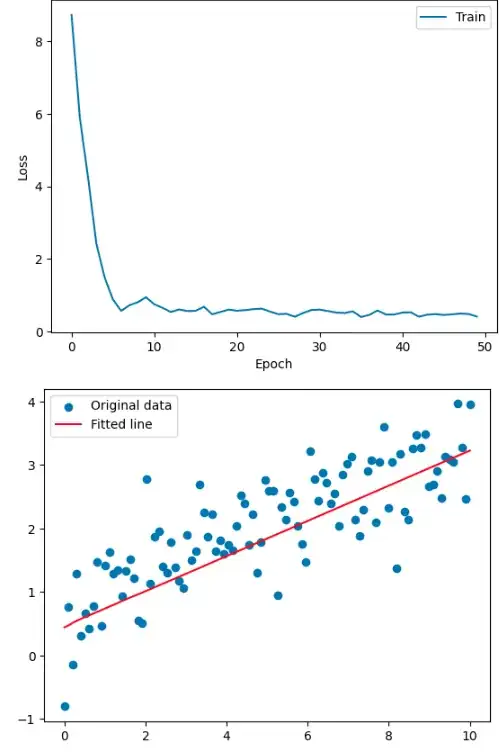
Plotting the loss
plt.plot(history.history['loss'])
plt.title('Model loss')
plt.ylabel('Loss')
plt.xlabel('Epoch')
plt.legend(['Train'], loc='upper right')
plt.show()
plt.scatter(x, y, label='Original data')
plt.plot(x, y_pred, color='red', label='Fitted line')
plt.legend()
plt.show()

As we see, in both cases it fails to capture the low x-value trend. I would like to ask if there are ways to improve this or other algorithms.

Memristor · Answer 1 · 2023-06-14T09:26:21.507

First: thanks for a great explanation, it is easy to help when the question is well posed. For the question per se: you can try a polynomial. Given the shape of your data I'd try a degree=3 polynomial, e.g.:

import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import Pipeline
Your data
x = np.array([ 0.        ,  0.1 ...])
y = np.array([-0.80373298,  0.76935298, ...])
Train the model
model = Pipeline([('poly', PolynomialFeatures(degree=3)),
                  ('linear', LinearRegression(fit_intercept=False))])
model.fit(x.reshape(-1, 1), y)
Plot
plt.scatter(x, y, label='Original data')
plt.plot(x, y_pred, color='red', label='Fitted line')
plt.legend()
plt.title(f"My model")
plt.show()

Other options would be:

A piecewise linear regression, e.g. using pypi: piecewise-regression
More on piecewise linear regression: stackoverflow: How to apply piecewise linear fit in Python?
Even more: datascience.stackexchange: segmented linear regression in python
Much more now with numpy: datascience.stackexchange: Python library for segmented regression (a.k.a. piecewise regression)
A step by step explanation for piecewise (using library pwlf): towardsdatascience: Piecewise Linear Regression Model
Using splines: scikit: Polynomial and Spline interpolation

improving Neural network regression model

Define the model

Compile the model

Train the model

Make predictions with the model

Plot the original data and the model's predictions

Preprocess data

Building the model

Compile the model

Train the model

Make predictions with the model

Plotting the loss

1 Answers1

Your data

Train the model

Plot