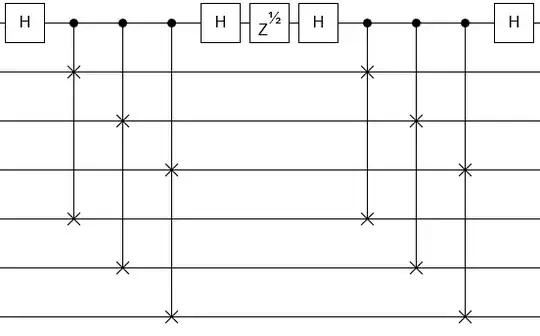
I am looking for an implementation using the quantum gates provided by the IBM composer of the following quantum function:
- input $2n$ qubits
- output $2n$ qubits wherein $50\%$ of the cases the state of the $2$ sets of $n$ qubits are swapped and in the other $50\%$ of the cases the state of the $2n$ qubits remain unchanged. With swapped I mean that qubit $q[i]$ will get the state of qubit $q[n+i]$ and qubit $q[n+i]$ will get the state of $q[i]$. Note also that all the qubits must be swapped or not.
E.g. $n=3$: If input $|000111\rangle$ then output in 50% of the cases is $|000111\rangle$ and in the other 50% of the cases is $|111000\rangle$
We have already a solution when $n=1$ in the following StackOverflow question:
but how can we do that when $n>1$?