Connected unbounded sets $S\subset \Bbb{R}^n$ such that $x\mapsto ||x||^t$ is uniformly continuous on $S$?

Question

Spending the night perusing my old answers, and this question left me wondering about the following.

Let's equip $\Bbb{R}^n$ with the usual Euclidean metric, and let us consider the map $N_t:\Bbb{R}^n\to \Bbb{R}$, $N_t(\vec{x})=||\vec{x}||^t$. The parameter $t$ is a positive constant, and the question I want to ask is:

For which pairs $(n,t)$ does there exist an unbounded path-connected set $S\subset \Bbb{R}^n$ such that the restriction $N_t\vert_S$ is uniformly continuous?

"Clearly" with $n=1$ we need $t\le1$. Path-connected + unbounded leaves no wiggle room for choice of $S$. The answers to the linked question give sets such that $N_2\vert_S$ is uniformly continuous, but those sets are not connected - hence this question.

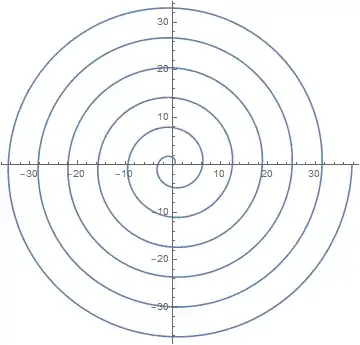
With $n\ge2$ the game is more interesting. I'm thinking of a $S$ as a path slowly spiralling outwards. With $n=2$ something like $S$ = Archimedean spiral, with the distance from the origin growing at the constant rate of one unit per each full revolution, looks good for showing that all $t\le2$ are ok. Here the length of the path in the $n$th loop is about $2\pi n$ meaning that if $\vec{x}$ moves by $<\delta$ the distance from the origin will change by approximately a constant times $\delta/n$. In that case $N_2(\vec{x})$ will grow from $n^2$ to $(n+K\delta/n)^2\approx n^2+2K\delta$, which is ok, just barely, for the purposes of uniform continuity.

It doesn't look nearly as promising for $t>2$. If we are spiralling out any slower, then further out the distance between consecutive rounds of the spiral will tend to zero. Looks like that makes uniform continuity an unrealistic goal, and

The argument by user147263 from the comments under the question shows that the exponent $t$ cannot exceed the dimension of the ambient space.

I haven't really thought about $n\ge3$. We can use the extra wiggle room by spending more time at about the same distance, like "nearly cover" the sphere at radius $n$ while gradually moving on to the sphere of radius $n+1$ and repeating ever after. But I don't know any good 3D-spirals, not forgetting $n$D.

Any thoughts? Ideas? Suitable higher dimensional spirals? Known work?

Answer 1

Let $r:(0,\infty)\to(0,\infty)$ and $\omega:(0,\infty)\to S^{n-1}$ be smooth smooth functions that define a curve $\gamma$ by $\gamma(s)=r(s)\omega(s)$ in spherical coordinates. I want to choose $S=\gamma((0,\infty))$, so I need to assume $r(s)\to\infty$ as $s\to\infty$. I will also assume $r$ to be increasing and $t$ to be positive.

Let $f(x)=\|x\|^t$. To ensure uniform continuity, I want the local Lipschitz constant of $f|_S$ at $\gamma(s)$, $$ L(s)=\frac{\frac{d}{ds}f(\gamma(s))}{\|\dot\gamma(s)\|}, $$ to be uniformly bounded. We have $$ \frac{d}{ds}f(\gamma(s)) = tr^{t-1}\dot r $$ and $$ \|\dot\gamma(s)\|^2 = \|\dot r\omega+r\dot\omega\|^2 = \dot r^2+r^2\|\dot\omega\|^2. $$ For the last equation, note that $2\omega\cdot\dot\omega=\frac{d}{ds}\|\omega\|^2=0$. Thus $$ L(s)^2 = t^2\frac{r^{2(t-1)}\dot r^2}{\dot r^2+r^2\|\dot\omega\|^2} = t^2\frac{r^{2(t-1)}}{1+(\|\dot\omega\|/\dot\ell)^2}, $$ where $\ell=\log(r)$.

For the Archimedean spiral $r=\omega=s$ we get $L(s)^2=t^2s^{2(t-1)}/(1+s^2)$, which stays bounded if and only if $t\leq2$. This was expected.

A uniform bound on $L(s)$ does not suffice for uniform continuity; if the "spiral" $S$ is too tight, $f|_S$ is not uniformly continuous. To make this issue easier to handle, let me assume that $\omega$ is periodic with some period $p>0$. I'm not sure if a periodic choice is optimal, but I have a vague feeling that an "optimal spiral" is periodic enough for the argument to work.

Note that if you want uniform continuity with respect to the path metric, bounding $L(s)$ is enough. If you want it w.r.t. the induced Euclidean metric, it is not.

Suppose we want Hölder continuity with exponent $\alpha\in(0,1]$. Then we get the requirement that $$ r(s+p)^t-r(s)^t\lesssim (r(s+p)-r(s))^\alpha. $$ (I don't want to keep track of multiplicative constants anymore, and I will assume $r$ to be so nice that I can make some approximations.) The function $r$ cannot grow too fast if we want $L(s)$ to remain bounded, so $$ r(s+p)^t-r(s)^t\approx t(r(s+p)-r(s))r(s)^{t-1} $$ should be a reasonable approximation. This combined with the above estimate gives $$ (r(s+p)-r(s))^{1-\alpha}r(s)^{t-1}\lesssim 1. $$ Approximating $r(s+p)-r(s)\approx p\dot r(s)$, we get $$ \dot r(s)^{1-\alpha}r(s)^{t-1}\lesssim 1. $$ This condition is not necessary for uniform continuity if $r(s+p)-r(s)$ has a uniform lower bound.

To make $L(s)$ bounded we should have $$ r^{2(t-1)} \lesssim (\|\dot\omega\|/\dot\ell)^2. $$ If we choose the parametrization so that $\|\dot\omega\|$ is constant, we end up with two requirements (if $r(s+p)-r(s)\to0$ as $r\to\infty$):

1. $\dot r^{1-\alpha}r^{t-1}\lesssim1$,
2. $\dot r r^{t-2}\lesssim1$.

Assuming $\alpha<1$ (which is not very restrictive), the first condition can be rewritten as $\dot r r^{(t-1)/(1-\alpha)}\lesssim1$. The condition then becomes $$ \dot r r^{\max\{(t-1)/(1-\alpha),t-2\}}\lesssim1. $$ If the spiral tightens up so that $r(s+p)-r(s)\to0$ as $r\to\infty$, the modulus of continuity of $N_t|_S$ should be as bad as that of $N_t$ in all of $\mathbb R^n$ (although this does not somehow show up in the calculation above).

It seems that the most promising way to go is to demand that $r(s+p)-r(s)\gtrsim1$ and $\dot r r^{t-2}\lesssim1$.

This answer is not conclusive, though...

Answer 2

(This is more of a "sketch proof" at the moment.)

The pairs are exactly $(t,n)$ with $t\leq n.$ The necessity was posted in a comment which I'll quote here:

For $t>n$ there is no such set: For all sufficiently large $k$ the set $S$ must contain a point $x_k$ with $\|x_k\|=k^{1/t},$ by connectedness. Since $N_t(x_k)=k,$ the points $x_k$ must be uniformly separated: there exists $\delta>0$ such that $\|x_k−x_j\|\geq\delta$ for all $k\neq j.$ For large $R,$ the ball $B(0,R)$ contains over $R^t/2$ points $x_k.$ Since the balls $B(x_k,\delta/2)$ are disjoint, it follows that $R_n\geq(R^t/2)(\delta/2)^n,$ which yields a contradiction when $R$ is large enough. – user147263

For $t=n$ there's no contradiction, but the balls $B(x_k,\delta/2)$ end up covering a positive proportion of $B(0,R).$ So the set isn't quite space-filling, but close: a $\delta/2$-neighborhood of the set covers a positive fraction of the space.

I'll just consider the $t=n$ case, because I want to reuse the letter $t.$ I'll assume $n\geq 2.$ (Perhaps interestingly, for $n\geq 3$ the construction can take place inside any cone with non-empty interior, in particular in $\mathbb R_{>0}\times \mathbb R^{n-1},$ whereas for $n=2$ unless I'm mistaken there is no unbounded connected subset of the upper half plane $\mathbb R_{>0}\times\mathbb R$ on which $N_2$ is continuous.)

Let $\mathbb T$ denote the metric space $\mathbb R/\mathbb 2\pi Z$ with the metric $d(x,y)=\min_{n\in\mathbb Z}|x+2\pi n-y|.$ There is a bilipschitz embedding $\phi$ of $\mathbb T\times [0,1]^{n-2}$ into the sphere $S^{n-1}.$ For $n=2$ this is just embedding a circle in a circle; for $n>2$ embed $\mathbb T\times [0,1]\to\mathbb R^2$ as an annulus, pass through the other coordinates to get an embedding $\mathbb T\times [0,1]^{n-2}\to\mathbb R^{n-1},$ then use stereographic projection $\mathbb R^{n-1}\to S^{n-1}.$

Start with the curve $\gamma(t)=(t,0,\dots,0)$ for $t>1$ - we'll modify this. For each odd integer $m>3,$ in the segment $m<t<m+1,$ the curve lives in a $(n-1)$-dimensional cube $[m,m+1]\times [0,1]^{n-2}.$ We can think of this as being a path through an $(n-1)$-dimensional $m\times m\times \dots\times m$ grid graph, with step size $1/(m-1),$ where the path starts in one corner and exits at another. Replace the curve within this cube by a Hamiltonian path with the same start and end - this is quite easy to construct. Smooth the corners. The important feature is that there are no significant "short cuts" smaller than $\Theta(1/m)$; specifically, for any two points at Euclidean distance $L<1/2m$ the arc length of the curve between these points is at most $L/2.$

Do the modification for each odd $m>3.$ Let $s(t)$ denote the following modified arc length: $$s(t)=\int_1^t \tau|\gamma'(\tau)|\;d\tau.$$

Then $s(t)$ increases by $\Theta(m^{n-1})$ during $m<t<m+2,$ which gives $s(t)=\Theta(t^n).$ Set $S_n=\{s(t)^{1/n}\phi(\gamma(t))\mid t>1\}.$ It should be clear that $S_n$ is unbounded and path-connected. I claim that $N_n$ is uniformly continuous on $S_n,$ in fact satisfying a kind of Lipschitz property on small scales. Consider $3<t<t'.$ We want to show $$|s(t)-s(t')|\leq C\|s(t)^{1/n}\phi(\gamma(t))-s(t')^{1/n}\phi(\gamma(t'))\|\tag{*}$$ for some large constant $C,$ whenever the right-hand-side is smaller than some small constant $c>0.$

The nice way for the right-hand-side to be small is when $|t-t'|<2$ and the quantity $L=|\gamma(t)-\gamma(t')|$ is at most $1/4t.$ Then because there are no "short cuts" we must have $|s(t)-s(t')|<2Lt.$ Using $s(t)^{1/n}=\Theta(t),$ the right-hand-side of (*) is $\Theta(Lt),$ which is perfect.

We need to rule out the possibility that the right-hand-side is small after looping around $\mathbb T$ a number of times. But this would only occur if $|t-t'|>2,$ which means $|s(t)-s(t')|>\Theta(t^{n-1}),$ which makes $|s(t)^{1/n}-s(t')^{1/n}|>\Theta(1).$ So the right-hand-side cannot be small this way.