1

Is the curve $y^2=x(x-1)^2$ an immersed submanifold in $\mathbb{R}^2$?

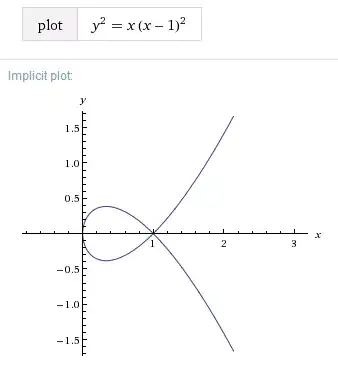
enter image description here

It's certainly not embedded since it intersects itself at $(1,0)$. I'm aware of techniques to prove a subset is not a immersed submanifold, but how can you find an appropriate topology and smooth structure to show this is immersed? It seems hard to pick one out of the blue.

Buble
  • 1,659
  • Very loose hint: can you find a parametrization of the curve? That will provide you with a mapping from $\mathbb{R}^1$ to your curve, and showing that that's an immersion should be straightforward. – Steven Stadnicki Aug 12 '14 at 21:29
  • @StevenStadnicki I could only find $t\mapsto (t,\sqrt{t(t-1)^2})$ when $t\geq 0$ and $t\mapsto (-t,-\sqrt{-t(-t-1)^2})$ when $t\leq 0$, but that traces out the curve differently. It's injective away from $0$ and $1$ but those are still problems. – Buble Aug 12 '14 at 21:45
  • It would be helpful to state what definition of "immersed submanifold" you're using. If it is "the image of a smooth immersion," then most of the answers here settle the question. But I have a feeling that might not be the definition you have in mind. – Jack Lee Aug 13 '14 at 14:05

2 Answers2

3

Yes, your curve is the image $\gamma (\mathbb R)$ of the global immersion $$ \gamma:\mathbb R \to \mathbb R^2:t\mapsto (t^2,t^3-t)$$

Edit
The idea for the parametrization comes from algebraic geometry:
Consider the one parameter family of lines $L_t=\{y=t(x-1)\}$ through $(1,0)$ and look at the other point of intersection of that line $L_t$ with the curve.
You obtain the point $P_t=(t^2,t(t^2-1))$ and the immersion (=parametrization) is the map associating to the slope $t$ of the line $L_t$ the point $P_t$.

Georges Elencwajg
  • 156,622
  • Thanks Georges. I see that $(t^3-t)^2=t^2(t^2-1)^2$. How did you come up with this immersion, or was it just inspection? – Buble Aug 12 '14 at 22:56
  • Algebraic geometers will notice that the result is purely algebraic and is valid over any field, even one where square roots do not always exist, like $\mathbb Q$ – Georges Elencwajg Aug 12 '14 at 22:56
  • Dear Buble, no it was not inspection but a standard technique in algebraic geometry to prove that a curve is rational by making use of its singularity. I'll try to sum up the idea in an Edit. – Georges Elencwajg Aug 12 '14 at 23:01
1

Let $c$ denote the curve in question, i.e. $c=\{y^2=x(x-1)^2\}\subset\mathbb{R}^2$. It is easy to verify that $c\setminus\{(1,0)\}$ is a smooth curve (around every point there is a neighborhood with a smooth parametrization). Furthermore, each one of the two "branches" at $(1,0)$ has a smooth parametrization. For example:

$$t\mapsto (t,\sqrt{t}(t-1))$$ and $$t\mapsto(t,-\sqrt{t}(t-1)).$$ Hence the answer is yes.

Amitai Yuval
  • 19,998
  • So is a manifold immersed if each point is in the image of a smooth parametrization? I only knew of the other implication. – Buble Aug 12 '14 at 21:53
  • Hmm. I'm not sure about the general case, but I think that the 1-dimensional situation is relatively simple. You can glue a few parametrizations to one another and obtain an immersion from the line to the plane. – Amitai Yuval Aug 12 '14 at 21:58
  • Oh, thanks. Btw, what is the parametrization at $(0,0)$, wouldn't the derivative be undefined there? – Buble Aug 12 '14 at 22:04
  • No, it wouldn't. Since the derivative of $x(x-1)^2$ is not $0$ at $x=0$, near $(0,0)$ $x$ is a smooth function of $y$. (implicit function theorem) – Amitai Yuval Aug 12 '14 at 22:07
  • If I can ask a qualitative question: Let's say you take that "loop" out of the graph and replace it with a straight line running from (0,0) to (1,0). Do you still have an immersed submanifold? Do you have a submanifold at all? – bob.sacamento Aug 12 '14 at 22:42
  • No, neither... This time the singular point is "more singular". – Amitai Yuval Aug 12 '14 at 22:48