3

To start off, I should clarify that the definition of immersed submanifold that I am using is the more restrictive one given by Lee. This says that $S\subseteq M$ is an immersed submanifold of M if it is endowed with a topology (not necessarily the subspace topology) with respect to which it is a topological manifold (without boundary), and a smooth structure with respect to which the inclusion map $\iota: S \hookrightarrow M$ is a smooth immersion.

So I am trying to determine whether $M_0 = \{(x,y)\in\Bbb{R}^2\mid y^2=x(x-1)^2\}$ is an immersed submanifold. Here is what it looks like. 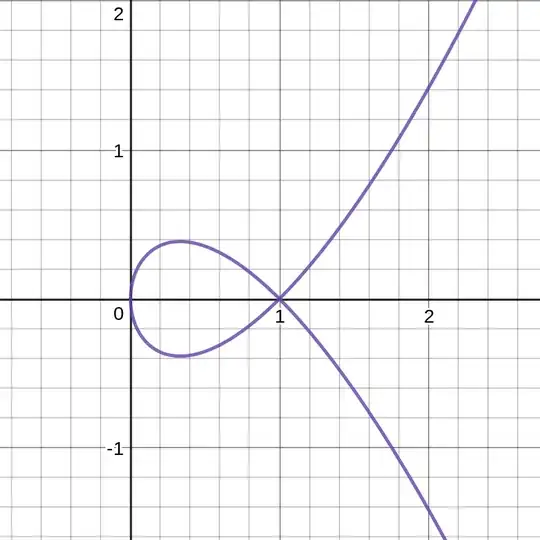enter image description here If we were to use the more relaxed definition of an immersed submanifold, i.e. the one that doesn't require injectivity, then we can can parametrize the curve as described in this question. But this parametrization is not injective because $-1 \mapsto (1,0)$ and $1 \mapsto (1,0)$.

My thinking is that in order for this set to be an immersed submanifold, we must show that we can parametrize the set with some smooth map $F:\Bbb{R}\to M_0$ that is injective and an immersion, and if this is not possible, then $M_0$ cannot be an immersed submanifold. Is this thinking correct?

Edit: As per AlexL's suggestion, it seems that I don't have to think of of just "parametrizations" from $\Bbb{R}$ to $M_0$. I could have a map from a disconnected manifold to the space.

luthien
  • 680

1 Answers1

4

Consider the manifold $M=\mathbb{R} \setminus \{ -1 \}$. Then one has a smooth immersion $j : M \to \mathbb{R}^2$ defined by $ t \to (t^2,t^3-t)$ that gives $M_0$.