4

I had an idea, that all geometric objects, that are different, as they're not a translation, rotation, and a reflection of one another cannot have the same area AND perimeter, as compared to ONE ANOTHER. They can't be CONGRUENT.

If the shapes are similar there is no similar shapes can contradict this "idea", or that is what I think.

I know that there was some idea on this, is there any theorem, or specific idea, which this is expressed?

hardmath
  • 37,715
Arbuja
  • 53
  • By geometric object do you mean "shapes" as in any sort of shape or is there something more specific you are getting at? – Sidharth Ghoshal Jul 24 '14 at 20:54
  • 1
    Are you suggesting that two figures with the same area and perimeter have to be congruent? That is certainly false. – Cheerful Parsnip Jul 24 '14 at 20:58
  • 1
    It can be any shapes that are not congruent. – Arbuja Jul 24 '14 at 20:59
  • Okay can this be shown! – Arbuja Jul 24 '14 at 21:00
  • 3
    Take any shape with area $S$ and perimeter $P$. You can find a rectangle with sides $A$ and $B$ such that $AB=S$ and $2A+2B=P$. –  Jul 24 '14 at 21:05
  • @Arbuja i am not sure if there is a name for this result – Sidharth Ghoshal Jul 24 '14 at 21:07
  • Another variation on your question which you might find interesting: Is it possible to construct a smooth family of distinct curves with the same perimeter and area? This should certainly be possible based on the examples below. – Semiclassical Jul 25 '14 at 00:23
  • @Semiclassical: Consider a circle with two independent "bumps"... –  Jul 25 '14 at 00:45
  • @Rahul: I see your point, though I would wonder about whether one could construct it smoothly in that case. I'm putting this together as a question in any case, so feel free to elaborate there. – Semiclassical Jul 25 '14 at 00:46
  • @Semiclassical: I'll save you the effort. Let the shape be given in polar coordinates by $r(\theta) = 1 + f(\theta-\alpha) + g(\theta-\beta)$ where $f$ and $g$ are bump functions, i.e. smooth and compactly supported. Now vary $\alpha$ and $\beta$ while the supports do not overlap. –  Jul 25 '14 at 00:48
  • @Rahul Too late! Plus what I'd most like to see is a family of algebraic curves with this feature. – Semiclassical Jul 25 '14 at 00:51

4 Answers4

10

Counter-example without words (except for these):

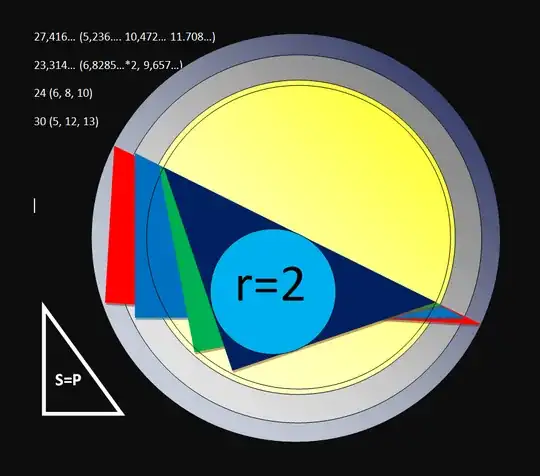
enter image description here enter image description here

Blue
  • 83,939
  • Note that this can be seen as a special case of a situation described in @hardmath's answer. – Blue Jul 24 '14 at 22:12
  • I should've seen the area as a bunch of segments, it was so simple, I just couldn't precieve it. Plus while I was walking I realized the same thing goes for a rhombus and square. Thanks once again @Blue for the truth. – Arbuja Jul 24 '14 at 22:41
  • 1
    Actually a rhombus and square with the same perimeter and area must be equal. All four sides of a rhombus are equal, and the square is a special case. So for the perimeters to be equal means the sides of the rhombus are the same as the sides of the square. Further, as a regular polygon, the area of the square is a maximum for quadrilaterals of a given perimeter, so if the rhombus area equals the square area, they must both be squares of equal sides, i.e. congruent. – hardmath Jul 25 '14 at 00:32
  • I almost agree! However, are the angles the same;)? – Arbuja Jul 25 '14 at 01:46
7

Another counterexample without words:

enter image description here

Greg Martin
  • 92,241
4

This idea is wrong, however attractive.

Let's consider a polygon with $n$ unequal sides. The side lengths determine the perimeter, so any rearrangement of the sides gives the same perimeter.

On the other hand any arrangement of the sides that inscribes the polygon in a circle maximizes the area contained by the polygon. The maximum area is independent of the order of sides, and even given reflection and rotation, there will be $n!/(2n)$ such arrangements, i.e. $(n-1)!/2$ noncongruent polygons, having the same area and perimeter.

On the other hand, restricting ourselves to two figures that are similar is a very narrow restriction. One has a single parameter of scale to vary between the figures. In that setting either equal area OR equal perimeter is enough to compel congruence of the figures.

For an example of two polygons with different numbers of sides, say 4 sides vs. 6 sides, consider a perimeter of six and area of two. We can achieve this with a rectangle of size $2 \times 1$. To match the perimeter we start with a regular hexagon having unit length sides, which will have area $\frac{3\sqrt{3}}{2} \gt 2$. We can maintain the perimeter at six but reduce the area down to two by "squeezing" a pair of opposing (parallel) sides closer together. The exact distance between these two sides to get the area six can be found by solving a cubic equation, but clearly the motion of moving sides closer together could achieve any area between that of the regular hexagon and zero (as the two sides get arbitrarily close).

hardmath
  • 37,715
  • Sorry, I need a more specific example. Like how you can arrange them and both are same, like a picture maybe. For some reason I can't envision it. – Arbuja Jul 24 '14 at 21:03
  • The smallest example is a quadrilateral. Pick four sides, make them different. I'll give you the example. – hardmath Jul 24 '14 at 21:04
  • 1
    Never mind I get it now, heron's formula for quadrilaterals stay the same, with both. Thanks! Aplogies:) – Arbuja Jul 24 '14 at 21:07
  • No problem, I just wanted to show how to generate examples with a large number of noncongruent variations. – hardmath Jul 24 '14 at 21:08
  • Hard Math: What about if the polygons have different number of sides, so one has 4 sides, and the other has 6 sides. Then can they still have the same perimeter or area? Is there some ways this could be improved. – Arbuja Jul 24 '14 at 23:09
  • I'm not sure how this is an improvement, but certainly two polygons can have the same area and perimeter but different numbers of sides. Of course two polygons with different numbers of sides are not congruent or similar. – hardmath Jul 24 '14 at 23:23
-2

The figure is a visual representation of four different possible right triangles satisfying the equality S=P

enter image description here

According to the results of calculations, the following numerical equalities of the area and perimeter of a number of two-dimensional figures were revealed: – of a square, when the side is 4 (the area and length of the perimeter, respectively, will be equal to the value 16), the radius of the inscribed circle is 2, and the described one is equal to the value 8, the diagonal of the square is equal to 32; – a circle, when the equality of the area and the length of the circle is observed at a value of 12.566 ... or 4 π (the radius of the inscribed circle is 2); – right-angled triangles with an irrational value of area and perimeter, when the area and length of the perimeter of the first is equal to the value 27,4163... ≡(√5+3)2 ( where the smaller catheter is 5,236... will be equal to √27.4163... or ≡√5+3, and the larger one is twice the value of the smaller one - 10.472 ..., the hypotenuse is 11.7082≡√45+5); the second, when the catheters are 6.8285... ≡√8+4, and the hypotenuse is 9.6568≡√32+4 with an area and perimeter value of 23.314... ≡(√8+2)2. The radius of the circle inscribed in the triangle is 2; – Heron triangles with sides: (5, 12, 13 and 6, 8, 10 are right–angled triangles) when the area and perimeter of the first is equal to the value of 30, and the second - 24; 6, 25, 29; 7, 15, 20; 9, 10, 17 ... ( obtuse triangles with an area of and the perimeter are equal to 60, 42, 36, respectively), the radius of the circle inscribed in the named triangles is 2; – an equilateral right triangle, with an area value of 20.7846... or =√3×12 (while the side length is 6.928...≡√48 or =√3×4), the radius of the inscribed circle is 2.

According to the results of calculations, the following numerical equalities of volume and area of a number of three-dimensional figures were revealed: – a cube with a face equal to the value of √8, the volume and surface area of the cube is 216, the radius of the inscribed sphere is 3; – spheres (equality of volume and surface area) equal to the value 113.097335526... or 36 π (in this case, the diameter of the sphere is 6, and its circumference is 18.85...≡6 π), the radius of the inscribed sphere is 3; – tetrahedron (equality of area and volume) equal to 374,123... ≡216×√3 (while the edge length is 14.669693845669907...≡√216), the radius of the inscribed sphere is 3; – octahedron (equality of area and volume) equal to the value 187.061... ≡108×√3 (while the edge length is 7.348669228349534...≡√54), the radius of the inscribed sphere is 3; – icosahedron (equality of area and volume) equal to the value 136.4595... (while the edge length is 3.9695...), the radius of the inscribed sphere is 3; – dodecahedron (equality of area and volume) equal to the value 149.8578... (while the edge length is 2.694168...), the radius of the inscribed sphere is 3; – cylinder (equality of area and volume) equal to the value 54π ≈ 169.646 ... (in this case, the radius is 3, and the height is double the value of the radius – 6). The area of the side surface is 113.097 ... (volume and area of the sphere inscribed in the figure) or 36π, and the area of one of the two bases is 9π, the radius of the inscribed The volume of the cylinder is equal to 3. The volume of the cylinder is exactly 1.5 times greater than the volume of the sphere inscribed in it (where there is equality of area and volume values); – a cone (equality of area and volume) equal to the value 96π ≈ 301.593... (in this case, the radius of the base is 6, the forming area is 10, and the height of the figure is 8). The area of the base (circle) is 113.097 ... (volume and area of the sphere inscribed in the figure) or 36π, the area of the lateral surface, respectively, – 60π, the radius of the inscribed sphere is 3; – a triangular pyramid (equality of area and volume of a tetrahedron) at a height of 12, the side of the base is 14.66969384567...≡√216 and is equal to the value 374.123..., the radius of the inscribed sphere is 3; – a four–sided pyramid (equality of area and volume) with a height of 12, the side of the base is 8.485281374...≡√72 and is equal to 288. The ratio of height to the side of the base is √2. At the same time, the area of the side surface of the pyramid is three times the area of the base (216 and 72), the radius of the inscribed sphere is 3; – a hexagonal pyramid with a height of 12, the side of the base is 4,898979485...≡√24 and is equal to 249.415..., the radius of the inscribed sphere is 3. Based on the calculations carried out, the conclusion is formulated: – in two-dimensional figures: square, circle, rectangular, obtuse and equilateral triangles, the radius of the inscribed circle with equal values of area and perimeter is 2; – in three-dimensional figures, tetrahedron, cube, octahedron, icosahedron, dodecahedron, cone, cylinder, 3-4-6-sided pyramid and sphere, the radius of the inscribed circle with equal values of area and volume is 3.

PolevaultScience PolevaultScie
  • 1