The Question.
I'm reading Lawson's "Inverse Semigroups: The Theory of Partial Symmetries" and I've hit something I don't understand. It's claimed on page 34 of my copy that
The category of complete, infinitely distributive inverse semigroups together with join-preserving homomorphisms forms a subcategory of the category of inverse semigroups and homomorphisms; indeed, the former is a reflective subcategory of the latter.
Let's call them $\mathbf{CompInfDist}_{\vee}$ and $\mathbf{InvSem}$, respectively.
What exactly is the left adjoint of the inclusion functor that makes $\mathbf{CompInfDist}_{\vee}$ reflective in $\mathbf{InvSem}$?
The Details.
This is technical stuff so let's have some definitions. Let $S$ be an inverse semigroup. Following Lawson . . .
Definition 1: The compatibility relation on $S$ is given by $$s\sim t\iff st^{-1}, s^{-1}t\in E(S),$$ where $E(S)$ is the set of idempotents of $S$.
Definition 2: A subset $A$ of $S$ is compatible if any pair of elements in $A$ are compatible.
The meet, $a\wedge b$, on $S$ for $a, b\in S$ is defined as the greatest lower bound of $a$ and $b$ with respect to the natural order on $S$; the join ($\vee$) is given dually. These extend to sets naturally.
Definition 3: We say $S$ is complete if every non-empty compatible subset of $S$ has a join.
Definition 4: We say $S$ is left infinitely distributive if, whenever $A$ is a non-empty subset of $S$ for which $\bigvee A$ exists, then $\bigvee sA$ exists for any element $s\in S$ and $s\left(\bigvee A\right)=\bigvee sA$. Then $S$ is infinitely distributive if it is both left and right infinitely distributive, where "right infinitely distributive" is defined analogously to left.
Now quoting MacLane,
Definition 5: A subcategory $\mathcal{A}$ of $\mathcal B$ is called reflective ($*$) in $\mathcal B$ when the inclusion functor $K:\mathcal A\to\mathcal B$ has a left adjoint $F:\mathcal B\to\mathcal A$.
My Attempt.
I'm completely at a loss. I'm sorry. I've written out all the relevant definitions on my whiteboard, including peripheral, easy ones like "functor", "adjoint", "subcategory", etc., but I just don't see it.
Anyway, thank you for reading all of this!
Please help :)
I've had an idea!
Definition 6: A subset $A$ of $S$ is permissible if it is a compatible order ideal. The set of all permissible subsets of $S$ is denoted $C(S)$.
Lemma 1: $C(S)$ (under multiplication of subsets) is an object of $\mathbf{CompInfDist}_{\vee}$.
"Proof": This is Theorem 1.4.23 of Lawson's book. $\square$
$\color{red}{\text{Perhaps}}$
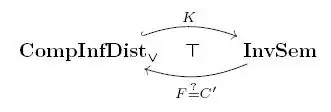 ,
,
where $F=C'$ is given by $C'(S\stackrel{f}{\to}T)=C(S)\stackrel{Cf}{\longrightarrow}C(T)$ for $Cf: C(S)\to C(T)$ given by $A\mapsto f(A)$. But this needs to satisfy $$\hom_{\mathbf{CompInfDist}_{\vee}}(C(S), Q)\cong_{\varphi_{(S, Q)}}\hom_{\mathbf{InvSem}}(S, K(Q)=Q)$$ for some natural bijection $\varphi_{(S, Q)}$.
Define $\iota: S\to C(S)$ by $\iota(s)=[s]$, where $[s]$ is the $\sim$-class of $s$.
Lemma 2: If $\theta: S\to Q$ is a homomorphism to an object $Q$ in $\mathbf{CompInfDist}_{\vee}$ then there exists a unique morphism $\theta^*:C(S)\to Q$ in $\mathbf{CompInfDist}_{\vee}$ given by $$\theta^*(A)=\bigvee\{\theta(a)\mid a\in A\}$$ such that $\theta^*\iota=\theta$.
"Proof": This is Theorem 1.4.24 of Lawson's book.$\square$
$\color{red}{\text{Maybe}}\,\varphi^{-1}_{(S, Q)}(\theta)=\theta^*$. But what's $\varphi_{(S, Q)}$ given by?
I'm not sure of the details :/
($*$) See the comments: I think this is the definition Lawson intended.