A limit question (JEE $2014$)

Question

The following is a JEE (A national level entrance test) question:

Find the largest value of the non-negative integer ( a ) for which:

$$ \displaystyle \lim_{x \to 1} \left( \dfrac{-ax + \sin(x-1) + a} { x + \sin(x-1) -1 } \right)^{\dfrac{1-x}{1-\sqrt x} } = \dfrac 1 4 $$

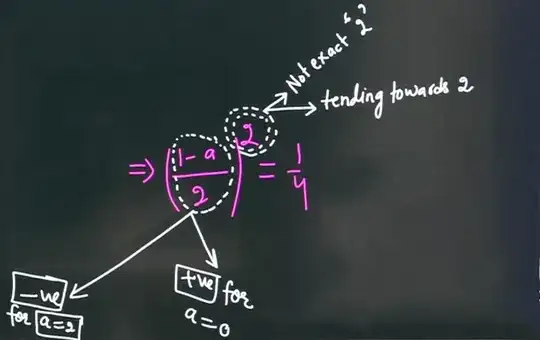
On solving this, we get $ a = 0 $ or $ a = 2 $. So we take the answer as $ 2 $. But the official answer key says that the answer is $ 0 $. The reason given (not in the official key - they simple contain the answer. I saw the reason in an "unofficial" solution to the question paper) is that if $ a = 2 $, then the term $\displaystyle \dfrac{-ax + \sin(x-1) + a} { x + \sin(x-1) -1 } $ tends to a negative value ( $-0.5$ ). So $ a = 0$.

BUT:

By putting $a = 2$ in the limit, and inputting that to wolframalpha (http://www.wolframalpha.com/input/?i=lim(+(+(-2x+%2B+2+%2B+sin(x-1)+)+%2F+(+x+-+1+%2B+sin(+x+-+1)+)+)+%5E+(+(1-x)%2F(1-sqrt(x))+)+)+as+x+tends+to+1), the answer turns out to be $0.25$. So, by putting $ a = 2$ also, we get the same value of the limit - $0.25$.

How to solve this dispute? Also, could you please check with Mathematica? Unfortunately, I don't have access to it!

(This is very important as the change in the answer key will affect the rankings in a dramatic way)

Answer 1

For $a = 2$, we have - writing $x = 1 + \delta$ - the expression

$$\left(\frac{\sin\delta - 2\delta}{\sin\delta + \delta}\right)^{\Large\frac{\delta}{\sqrt{1+\delta}-1}}.\tag{1}$$

For most $0 < \lvert\delta\rvert < 1$, the exponent is not a rational number.

So the question is: Does raising a negative real number to a non-rational power make sense or not?

If you have no qualms about using complex numbers (like Wolfram), the expression makes sense, and the limit as $\delta\to 0$ is $\frac{1}{4}$, no problem.

The makers of the test apparently had qualms about using complex numbers and decided that the expression $(1)$ doesn't make sense in general.

Answer 2

Let's study the base of the exponential: $$ \lim_{x\to1}\frac{-ax+\sin(x-1)+a}{x+\sin(x-1)-1}\overset{\mathrm{H}}{=} \lim_{t\to0}\frac{-a+\cos(x-1)}{1+\cos(x-1)}=\frac{1-a}{2} $$ (“H” denotes an application of l'Hôpital's theorem). Thus the limit is non negative only for $a\le1$. In particular, being the base continuous after extending it to $0$ with the limit, if $a>1$ there is a neighborhood of $1$ where your function is not defined (the basis of an exponential must be non negative).

The limit now poses no problem, because the exponent is $1+\sqrt{x}$ (for $x\ne0$), so your limit is $$ \left(\frac{1-a}{2}\right)^2 $$ which is equal to $1/4$ if and only if $$ \left(\frac{1-a}{2}=\frac{1}{2} \quad\text{or}\quad \frac{1-a}{2}=-\frac{1}{2}\right) \quad\text{and}\quad a\le1 $$ that is, $a=0$.

Answer 3

Whatever the (finite) limit inside the main parenthesis ($\frac{1-a}2$), the limit of the exponent is $2$ (it simplifies to $x+\sqrt x$), and the full expression is positive.

Solution: $a=2.$

UPDATE:

The power of a negative (when $a=2$) can be dealt with with complex logarithms: $$\lim_{x\rightarrow1}\ln(-|f(x)|)^{g(x)}=\lim_{x\rightarrow1}(g(x)(\ln |f(x)|+i\pi))=\lim_{x\rightarrow1} g(x)\lim_{x\rightarrow1}(\ln |f(x)|+i\pi)=2\ln\frac12+2i\pi.$$

Answer 4

The official answer is correct.

Indeed, we have $$\lim_{x\to 1}\frac{\sin(x-1)-a(x-1)}{\sin(x-1)+(x-1)}=\lim_{x\to 1}\frac{\cos(x-1)-a}{\cos(x-1)+1}=\frac{1-a}{2}$$ Thus, if $a=2$, the base is negative in a neighbourhood of $1$, and, unless you consider complex exponentiation, you can't raise a negative number to an irratioanl number.

Answer 5

See this

After simplification of question it becomes $\displaystyle{\left(\frac{{{1}-{a}}}{{2}}\right)}^{{{t}{e}{n}{d}{s}\to{2}}}$

$\displaystyle^{\left({t}{e}{n}{d}{s}\to{2}\right)}$ because the power after simplification is $\displaystyle{1}+√{x}$ and $\displaystyle\lim_{{{x}\to{1}}}$

Now number tends to 2 can be 1.99999999999999 which can be written as 199999999999999/100000000000000 which is basically Odd Integer/Even Integer thus a possibility of undefined if a = 2

If a=0 then the question is (+ve)^<tends to 2> Therefore defined!

Thus a=0!!