26

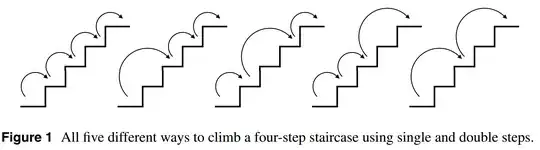
I came across an interesting puzzle:

You are climbing a stair case. It takes $n$ steps to reach to the top. Each time you can either climb $1$ or $2$ steps. In how many distinct ways can you climb to the top?

Is there a closed-form solution to the problem? One can compute it by creating a 'tree' of possibilities of each step. That is, I can either take 1 or 2 steps at each stage and terminate a branch once it sums to $n$. But this is would get really unwieldy very quickly since the maximum number of nodes in a binary tree is $2^{n+1}-1$, i.e., exponential. Is there an easier way to solving this puzzle?

vonbrand
  • 28,394
PhD
  • 2,861

4 Answers4

45

Let $F_n$ be the number of ways to climb $n$ stairs taking only $1$ or $2$ steps. We know that $F_1 = 1$ and $F_2 = 2$. Now, consider $F_n$ for $n\ge 3$. The final step will be of size $1$ or $2$, so $F_n$ = $F_{n-1} + F_{n-2}$. This is the Fibonacci recurrence.

fahrbach
  • 1,843
  • 3
    Ha! Some simple and yet a convoluted formation of the sequence. That explains it. Can't believe I couldn't see it :) – PhD May 11 '14 at 01:53
  • Is it possible to generalize it? Such as what if your steps are 2, 3, and 5? Also, we can compute fibonacci in matrix form which is faster. In the case of 2,3 and 5 steps, what would be the closed form solution? – Bagus Trihatmaja Dec 05 '18 at 08:53
  • 1
    Yes, this falls into the more general framework of solving linear recurrence equations. They always admit fast evaluations via matrix exponentiation and often have closed-form solutions, especially when the characteristic equation has low degree since you need to find all of its roots. – fahrbach Dec 06 '18 at 22:19
  • Can someone help me understand a tweak to this problem where the order of the steps doesn't matter? How to come up to a closed form equation for it? – mankadnandan May 26 '19 at 07:38
  • 2
    @mankadnandan if the order doesn't matter then you are just counting the number to partitions of $n$ into parts of size $1$ and $2$ https://en.wikipedia.org/wiki/Partition_(number_theory) – Condo Apr 23 '21 at 15:18
26

The solution to this problem indeed corresponds to the Fibonacci numbers, as mentioned by @fahrbach.

Here is an illustration of what you are trying to solve for the case of $n=4$ steps (taken from this website, which also gives a combinatorial solution)

enter image description here

Any staircase with $n$ steps allowing paths with increments of 1 or 2 steps at a time will end up in one of two states before the last path is taken: either we've climbed $(n-1)$ steps already and have $\color{red}{one}$ more step to take, or we've climbed $(n-2)$ steps already and we have $\color{blue}{two}$ more steps to take (if we took only one step here then we'd end up in an arrangement from the first state).

enter image description here

Thus, to get the total number of possible ways to climb $n$ steps, we just add the number of possible ways we can climb $(n-1)$ steps and the number of possible ways we can climb $(n-2)$ steps, giving the familiar recurrence relation:

\begin{equation*} F_n = \left\{ \begin{array}{l@{}l@{}l} 1 & n = 0,1\\ \color{red}{F_{n-1}} + \color{blue}{F_{n-2}} & n \ge 2 \end{array} \right. \end{equation*}

Josh Broadhurst
  • 549
  • Can this answer be expanded to answer the question "Given a set of possible step sizes S, calculate the number of possible ways you can climb n steps using step sizes in S)"? – Ephraim Nov 04 '15 at 20:21
  • 1
    @Ephraim That's simple, it's just $F_n=\sum_{i\in I} F_i$ where $I$ is the set of steps that can jump to step $n$. – Stella Biderman Jan 31 '17 at 16:37
  • 1
    This is the explanation that clicked to me, the colored figure makes a lot of sense, thanks. – neevek Oct 20 '20 at 16:47
  • 1
    So, if the there is 0 stairs then there is 1 way to climb it ? – yusuf tezel Apr 28 '22 at 13:03
2

We can change this question into: In how many ways is possible to write a number as the ordered sum of 1s and 2s?

We can prove this using direct proof.

Hypothesis: For Fibbonaci number $F_1=1, F_2=1, F_{n}=F_{n-1}+F_{n-2}$, $Q(k)=F_{k+1}$

We say that we have constructed every order of $Q(n)$. Then, we construct $Q(n+1)$ this way:

  1. For all orders, we add $+1$ to change $n$ to $n+1$. (There are now $Q(n)$ numbers.) Note: all numbers that are constructed here ends in $+1$.
  2. For all orders that end with $+1$, we change it to $+2$. We shall prove that the amount will be $Q(n-1)$ to complete the proof. Note: all numbers that are constructed here ends in $+2$.

It can be seen that by constructing in this way there contains all orders.

Proof of step 2: If we constructed $Q(n)$ in the way above, then all numbers ended in $+1$ will be the amount $Q(n-1)$ by step 1. above, and we are done.

Vee Hua Zhi
  • 893
1

This is the Fibonacci numbers - One interpretation of the n-th Fibonacci number is the number of ways to compose $n$ with parts in $\{1,2\}$ (that is, the n-th fibonacci number counts the number of sequences whose values are in $\{1,2\}$ whose sums are $n$). This is often called "Golfs and Cadillacs" or something similar.

Batman
  • 19,790
  • Could you please elaborate as to "how" it helps solve the problem? – PhD May 11 '14 at 01:46
  • If there are $n$ steps, you have $F_n$ ways to reach the top of the stairs? The sequences map directly to the amount of stairs you climb with each step. I don't see how it can be any clearer. This interpretation can be used as a definition of the Fibonacci numbers and can be shown to be equivalent to the recurrence by using a straightforward combinatorial argument. – Batman May 11 '14 at 01:47
  • I see what you mean. Perhaps what I'm confused by is by this: that is, the n-th fibonacci number counts the number of sequences whose values are in {1,2} whose sums are n. Could you please provide an example to explain this? – PhD May 11 '14 at 01:49
  • You form a sequence made up of 1's and 2's whose sum is $n$. For example, for $n=3$, the sequences are (1,1,1), (1,2) and (2,1) giving you 3 ways to climb the stairs. Note that this is the common combintorics use of Fibonacci numbers, which is offset by 1 from the kind you learn in elementary school (this Fibonacci sequence is $1,2,3,5,...$ instead of $1,1,2,3,5,...$). – Batman May 11 '14 at 01:51