This question is a "corollary" (if you will) to the World's Hardest Easy Geometry Problem (external website). Formally, this is called Langley's Problem. The objective of that problem was to solve for angle $x^{\circ}$, with the given angles of $10^{\circ}, 70^{\circ}, 60^{\circ}, 20^{\circ}$. Someone presented a solution to that problem. Here's also a rather colorful and interactive solution to a problem like this, but with different angles.
Now, I wanted to generalize this problem, replacing the angles of $10^{\circ}, 70^{\circ}, 60^{\circ}, 20^{\circ}$ with angles of $W^{\circ}, X^{\circ}, Y^{\circ}, Z^{\circ}$, respectively (see below picture).
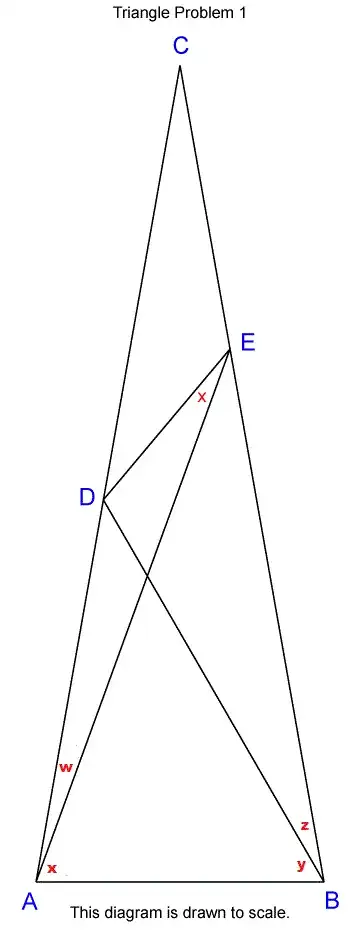
How can we derive an analytical expression of angle $x^{\circ}$, in terms of $W^{\circ}, X^{\circ}, Y^{\circ}, Z^{\circ}$?

