This is a variation of the notorious Langley's problem.
We follow a trigonometric approach. Let $\angle BDE=x$.
i) Use the Law of sines in $\triangle EBC$,
$$\frac{\sin 25^\circ}{EB}=\frac{\sin75^\circ}{AB}.$$
ii) Use the Law of sines in $\triangle DBC$,
$$\frac{\sin 80^\circ}{BD}=\frac{\sin 35^\circ}{AB}.$$
iii) Use the Law of sines in $\triangle EBD$,
$$\frac{\sin x}{EB}=\frac{\sin (165^\circ-x)}{BD}=\frac{\sin (15^\circ+x)}{BD}.$$
It follows that
$$\frac{\sin (15^\circ+x)}{\sin x}=\frac{\sin 80^\circ}{\sin 35^\circ}\cdot \frac{\sin 75^\circ}{\sin 25^\circ}$$
Since $\sin (15^\circ+x)=\sin 15^\circ\cos x+\cos 15^\circ\sin x$,
we obtain that
$$\cot x=\frac{1}{\sin 15^\circ}\cdot\frac{\sin 80^\circ}{\sin 35^\circ}\cdot \frac{\sin 75^\circ}{\sin 25^\circ}-\cot 15^\circ.$$
Therefore $x=5^\circ$.
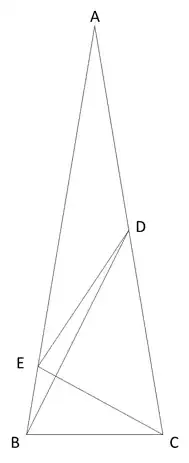 So far I figured out that $\angle BDE=\angle AED-15^\circ$ and $\overline{BD}\bot\overline{CE}$ that don't seem to be helping.
So far I figured out that $\angle BDE=\angle AED-15^\circ$ and $\overline{BD}\bot\overline{CE}$ that don't seem to be helping.