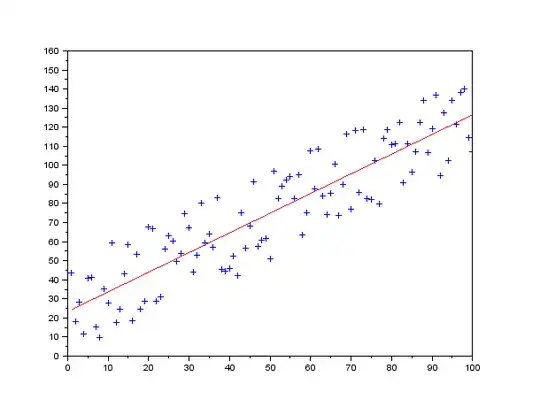
I have array of random numbers. How can I calculate linear regression segment? I am interested in finding the exact formula so I be able to use it in my work, please help me finding this formula with the next declarations:
- $N$ - the number of random numbers in the array
- $S$ - the sum of the numbers in the array.
- $array_{min}$ - the minimum number in the array
- $array_{max}$ - the maximum number in the array
- $E$ - the average number in the array.
We are looking for $y = mx + c$. So you need to find a formula to represent $m$ and $c$ with the above declarations.
The array of random number are the $Y$. $X$ is just neutral numbers from $0$ to $N$