4

I came across the problem of computing the homology groups of the closed orientable surface of genus $g$.

Here Homology of surface of genus $g$ I found a solution via cellular homology. This seems to me like the natural way of calculating something of this sort although I know that it is also possible to do this using the Mayer-Vietoris sequence.

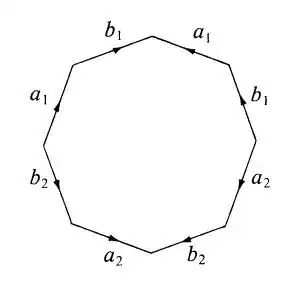
I understand the main calculations of the solution referred to above, however the CW-structure that the surface of genus $g$ is endowed with is a mystery to me.

I understand it for the case $g=1$ where it is quite conceivable in a graphic manner.

Could someone please explain what is going on for $g \geq 2$?

Thanks in advance for any help.

Community
  • 1
Tom Bombadil
  • 1,746

2 Answers2

6

I always found the "$4g$-gon with identified sides" approach mysterious until I watched this video. Basically, you can construct a genus $g$ surface by gluing a genus 1 surface to a genus $g-1$ surface.

At around 1:00 in the video, the speaker shows how to make a 2-holed torus by taking two 1-holed tori (i.e., rectangles with opposite sides identified), cutting them at the corner and pasting them together. I think you can continue this process recursively to get orientable surfaces of higher genus. So to get a genus 3 surface, you would take the octagon you had for a genus 2 surface, a torus (rectangle), cut them both at a corner and glue them together.

Viktor Vaughn
  • 20,897
3

Basically you can construct the surface of genus $g$, by gluing a disk $\mathbb{D}^2$ to a wedge of $2g$ circles, $\bigvee\limits_{i=1}^{2g} \mathbb{S}_i^1$. First we think the border of $\mathbb{D}^2$ as $2g$-sided polygon, and we put labels in each side $a_1,\ b_1,\ a_1,\ldots,\ a_g,\ b_g$, and arrows as in the picture: Case $g=2$

Then we label each copy $\mathbb{S}^1_i$ and give it an orientation, starting with $a_1$, followed by $b_1$, etc. until we label the last on $b_{g}$. Then we identify $\partial\mathbb{D}^2$ with $\bigvee\limits^{2g} \mathbb{S}^1_i$, matching the letters, $a_i,\ b_i$ and the orentations. In other words we are giving an identification on $\partial\mathbb{D}^2$, by $a_1b_1a_1^{-1}b_{1}^{-1}\cdots a_g b_g a_{g}^{-1}b_g^{-1}$.

So returning to your question about the CW complex structure, we have just given above one structure that consists:

$(a)$ One $0$-cell structure: a point.

$(b)$ $2g$ $1$-cell, that form the $1$-skeleton, which is: $\bigvee\limits^{2g}\mathbb{S}^1_i$

$(c)$ One $2$-cell: the disk $\mathbb{D}^2$.

Picture taken from Greenberg's Algebraic topology

D. Corro
  • 320