Gluing diagrams for tori

Question

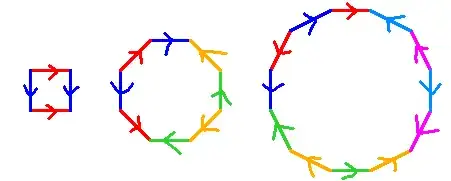
I know that gluing opposite sides of a square gives a torus, and I think I've seen somewhere that gluing opposite sides of an octagon gives a 2-holed torus. Is there a general way of constructing gluing diagrams for surfaces of genus $g$ / for $k$-holed-tori?

Answer 1

Here's a depiction of the most common construction:

Gluing a 4k-gon by grouping the edges into groups of 4 like this produces a k-holed torus. Other gluings of 4k-gons also produce a k-holed torus, as long as they keep the surface orientable and ensure that all 4k vertices are glued together into a single point. This is a consequence of Euler's formula for CW complexes and the classification theorem for closed 2-manifolds. Gluing opposite sides together, as you suggest, works as well.