4

I've read that in a negatively curved space (hyperbolic space), the measured circumference of a circle is greater then the expected circumference. But I can't just imagine that virtually. Can anyone help?

astronomy olampiadist
  • 43

2 Answers2

4

Not an answer, but very often, the behavior in hyperbolic space differs from Euclidean in the opposite way to the behavior on the sphere. Like: the sum of the angles of a triangle is greater than $\pi$ on the sphere, less in hyperbolic space. It’s the same with the circumference of a circle: on the unit sphere, if the your radius-segment (on the surface) is of length $\ell$, the distance (through the solid ball) between the ends of the diameter is $2\sin\ell$. (If you have trouble seeing this, slice the ball through this diameter, so that you’re talking about the ends of an arc of length $2\ell$.) The circle on the surface of the ball has genuine radius $\sin\ell$, so that the circumference is $2\pi\sin\ell$, always less than $2\pi\ell$.

Now, you expect that the same formula will work in the hyperbolic plane, except that you replace the trig function with a hyperbolic function. And indeed, the circumference of the circle now is $2\pi\sinh\ell$, always greater than $2\pi\ell$.

Lubin
  • 65,209
  • Thanks for your answer. Is there a generalized formula for the circumference of a circle, when given the curvatures along the x and y axes? – Cameron Hudson Feb 17 '24 at 23:57
  • Sorry, @CameronHudson, you’ll have to ask somebody that really knows what they’re talking about, not me. – Lubin Feb 18 '24 at 21:00
3

I think if you draw a (small, somewhat awkwardly distorted) circle on a saddle-type surface (the point $X$ in the image below), you will find that it has the desired property.

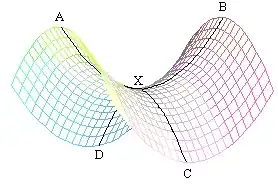
Saddle geometry

You can imagine to yourself that going from $A$ to $B$ in a circular path passing through point $C$ is a much longer path than the half-circumference of a cirlce with diameter $XC$. This is because of how the region between the lines $XB$ and $XC$ are "flayed out"

In a hyperbolic space, every point behaves locally like the saddle.

lionelbrits
  • 174