3

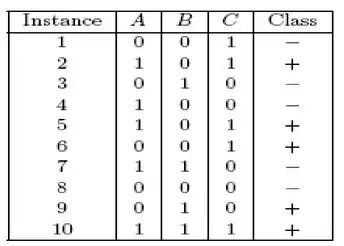
enter image description here

Are A and B conditionally independent given the class label?

I calculated that

$$P(A=1) = \frac{1}{2}$$ $$P(B=1) = \frac{2}{5}$$ $$P(A=1,B=1)=\frac{1}{5}$$

My answer is yes. I do it by anding $(A\text{ and }B)$ which shows that when $A = 1$ and $B = 1$ it doesn't imply Class will be +. How can I actually prove this without this pseudo prove I have come up with?

Michael Hardy
  • 1
Mike John
  • 174

2 Answers2

0

A and B are conditionaly independent of C iff for every value of C, $P(A\cap B|C) = P(A|C)P(B|C)$

Lets try class = +.

$P(A\cap B|+)=\frac{P(A\cap\ B \cap +)}{P(+)} = \frac{1}{5} \neq P(A|+)P(B|+) = \frac{3}{5}\frac{2}{5} = \frac{6}{25}$

So no, they are not.

-1
  1. Marginalize to get the mass functions $p_{A \mid CL}(a \mid cl),p_{B \mid CL}(b \mid cl)$ and $p_{A,B \mid CL}(a,b \mid cl).$
  2. Check for every class label $CL=cl$ and $\forall a,b$ if the following holds (this is the definition of conditional independence of independence in general):
    $p_{A,B \mid CL}(A=a,B=b \mid CL=cl) = p_{A \mid CL}(A=a \mid CL=cl)p_{B \mid CL}(B=b \mid CL=cl)$
    If it holds, then $A,B$ are conditionally independent of the class label $CL$
Sudarsan
  • 876