Maximum amount willing to gamble given utility function $U(W)=\ln(W)$ and $W=1000000$ in the game referred to in St. Petersberg's Paradox?

Question

The game works as such: I flip a fair coin until it lands on tails. $h$ is the number of heads obtained until the first tail occurs and the game stops. My payoff from this game is:

$\hat G=2^{h}$

I have a utility function $u(W)=\ln(W)$ and $W=1000000$ in initial wealth. I want to find the maximum amount, $F$, I should be willing to pay to play this game.

I know that $E(U(W-F+\hat G)=U(W)$ and I need to solve that equation for $F$. This is:

$E[\ln (1000000-F+2^{h})]=\ln(1000000)$

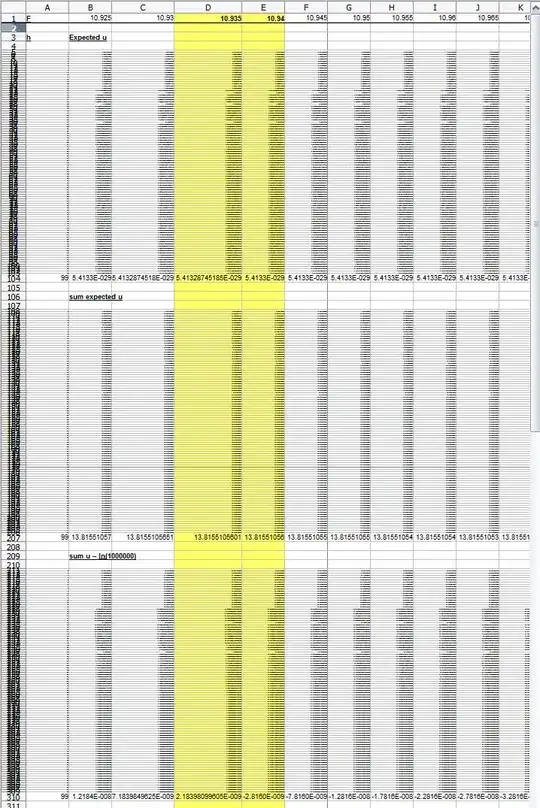
As I believe the geometric distribution would be best for modeling this game(as $h$ is essentially the number of trials before the 1st "success", or in this case, failure), I use the pdf of the geometric distribution (with $p=\frac{1}{2}$ assumed) to try to solve for the expected value. Thus, I end up with this:

$\displaystyle \sum_{h=0}^{\infty}\ln(1000000-F+2^h)\cdot\left(\frac{1}{2}\right)^{h+1}=\ln(1000000)$

However, I'm not sure where to go from here. Any guidance would be appreciated. Am I even approaching this problem in the correct way?

Answer 1

I see no flaw in your reasoning. Unfortunately it leads to an equation that you (and I, and maybe everyone) cannot solve explicitly. So you might need to solve using computational method. This can be done using OpenOffice Calc for instance, and shows that the maximal $F$ is between 10.935 and 10.94, hoping that I encoded the formula right (the very small line are the computations for h going from 0 to 98):

Notice that the wikipedia article on the paradox treats explicitly the question of the maximum price a millionaire would be ready to pay with log utility (under the section "Solving the paradox) and gets the same result of $10.94, which is reinsuring. If, as I did when I first saw it, you have a doubt on whether the formula in the wikipedia article is the same as the one you propose, see this question : Mistake in Wikipedia article on St Petersburg paradox?