I know there are lots of related questions on here, but I can't seem to find what I'm looking for.
Given some event with, say, a $1$ in $1{,}000{,}000$ probability (e.g., $7$ being chosen randomly as a number between $1$ and $1{,}000{,}000$), I'd like to get a rough idea of the probability of seeing that event happen at least once in $1{,}000{,}000$ trials. (The temptation is somehow to say that you get roughly even odds.)
I understand that the probability of seeing a $1$-in-$n$ event occur at least once in $n$ trials is simply $1 - \frac{(n-1)^n}{n^n}$, but when $n$ is large, computing such values is difficult (for me at least).
Hence I'd like an idea as to whether this converges as $n$ approaches infinity.
Just from playing around with some values up to ($n=144$), it seems that the value converges towards $\sim0.633$.
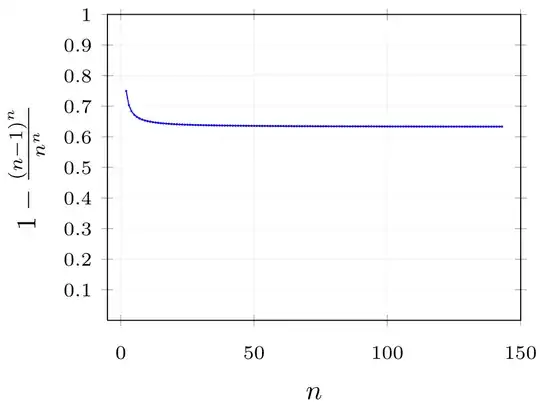
So my questions relate to understanding this more.
- Does this value indeed converge?
- If so, does the resulting value have any significance?
- Conversely, for an event with a 1-in-$n$ chance, is there a way to characterise (in the general case) how many trials would be needed to see such an event at least once with $p\approx 0.5$?