22

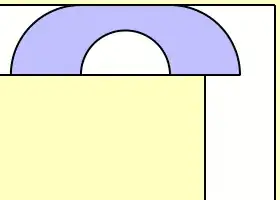
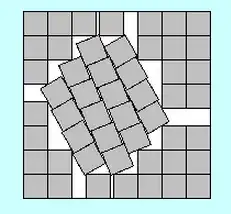
I was surprised to learn that both for the Moving Sofa Problem and Packing 11 Squares solutions have been proposed, but in either case the optimality of the proposed solution is, as of yet, only conjectured. At first glance, these problems appear "innocent" to me, but presumably deceptively so. (Rest assured: I don't have clue on how to approach either of them.)

What is the nature of the presumed hurdle that needs to be taken here to prove optimality? Is the issue some kind of computational complexity that needs to be overcome, does it require some technique that as of yet is unknown, does the optimality hinge on some other conjectures, ...? Or is this something we don't and cannot know until it actually has been done?

I realize that these are two different problems, but, I thought, perhaps unwisely, to put them in one question. Perhaps they share a difficulty that is shared by many such problems and still is rather specific to such problems.

Further references: Moving Sofa Problem on Wikipedia, Moving Sofa Problem on MathWorld, Gerver solution to the Moving Sofa Problem (pdf), Packing 11 Squares on MathWorld

I include an animated image by Claudio Rocchini of (unfortunately) a non-optimal solution to the first problem. Just because it looks good.

enter image description here

Community
  • 1
Řídící
  • 3,268

1 Answers1

25

This is an inadequate answer, but...

These problems are difficult because (a) the space of possible solutions is vast, and (b) there seems insufficient structure to reduce the space so that searching it becomes feasible.

Consider the 11-squares problem. Each square has a location and an orientation, and so can be pinned down by specifying three parameters. So 33 parameters determine a configuration of 11 squares, and so determine the surrounding square. But this means one is, in a sense, searching a 33-dimensional space for the optimal solution.

Of course, there are many constraints that make this 33 an overestimate. (For example, the first square can be constrained to, say, $(0,0){-}(1,1)$, so it is really "only" a 30-dimensional space...) But when you see a packing like that shown below (due to Károly Hajba), your confidence in constraining the parameters is shaken.


     SquarePacking
     (A packing of 51 squares. Image from this link.)

Joseph O'Rourke
  • 31,079
  • 9
    (1) Excellent answer. (2) That 51-square packing is pretty frightening! – user43208 Oct 20 '13 at 19:17
  • 1
    +1 Thanks. Don't you think that there is some topology-like characterisation of any solution? – Řídící Oct 20 '13 at 19:34
  • @aufkag: I am not sure what a "topology-like characterization" would be. In the squares problem, certainly the nonoverlap of any pair of squares leads to algebraic constraints that carve into that 33-dimensional space... – Joseph O'Rourke Oct 20 '13 at 19:44
  • @JosephO'Rourke What I mean is, that the 51-solution (besides immediately allowing for 31 similar solutions) seems to have a clear 18 (slanted)-33 (straight) character. That seems like structure. – Řídící Oct 20 '13 at 19:45
  • @aufkag: OK, I see. Certainly while searching one might search for $k$ slanted and $n-k$ straight, but still one would presumably have to check this for each $k$. – Joseph O'Rourke Oct 20 '13 at 19:48
  • @JosephO'Rourke More structure is to be found in (the counts of) the "types" of touchings between squares. (I wouldn't know if that would help, but still.) – Řídící Oct 20 '13 at 19:58
  • 2
    @aufkag: It is not even known if those solutions are optimal, though. – BlueRaja - Danny Pflughoeft Oct 20 '13 at 22:39