I am working on a simulation of a two-wheeled robot, and at present am driving it by setting each individual wheel's velocity. The robot is similar to an ePuck:

What I would like to do is set an initial (and constant) overall speed for the robot, and simply command it to turn by a specified angle while moving. At this point, I'd like to keep the model simple and not worry as much about acceleration.
Essentially, what I would like to do is command it to turn by 90 degrees, as shown in the next picture. On that basis, with a constant speed on the forward motion of the body itself, what I'd like to know is how to calculate the appropriate velocity of each wheel separately.
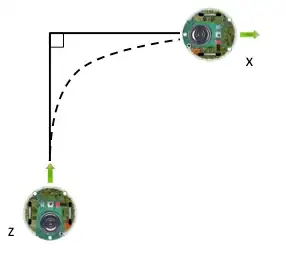
I'd looked into some existing models that go into differential equations here and here, however I wasn't able to understand if it were possible to find the values that I'm interested in.