2

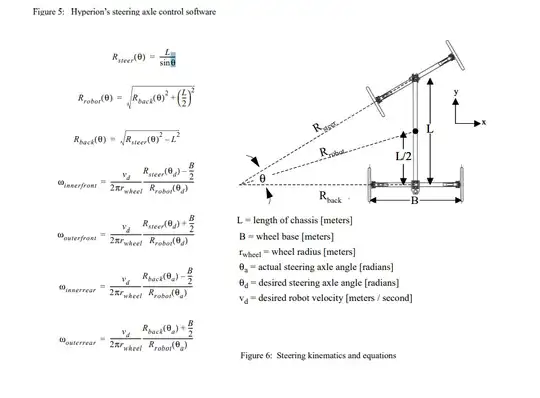
I would like to build a small robot. The robot will have 4 independent motors, one for each wheel. It will have a rear axle fixed and the front axle will be freely pivoting around its center, somewhat like in the image below.

enter image description here

Source:https://www.ri.cmu.edu/pub_files/pub3/shamah_benjamin_2001_1/shamah_benjamin_2001_1.pdf When I tried calculating the speed of the wheels using the formulas in the image, I did not get the expected result (if as input I choose 1.5708 radiant as "Rsteer", the resulting speed for the rear wheels are both positive, while I was expecting one wheel to have opposite speed of the other, to permit the robot to rotate around the center of the rear axle.

I am not sure the formulas are correct or complete. Is there a way to calculate te speed for all four the wheels at different speed and angle of turn for this configuration of wheels? Could you please me point me in the right direction to understand the math involved in this calculation?

I've also looked at similar questions here like: here here here and here , but still I am not able to understand how to solve this problem.

Cesareo
  • 36,341
user1937747
  • 121
  • 1
    $R_{\rm steer}$ is a radius, a length. Why do you want to treat it as an angle? The car rotates around the center where the letter $\theta$ is written, the intersection of the axis lines. Why should the speeds of the wheels have opposite signs? The car is not turning in-place. – Lutz Lehmann Dec 09 '21 at 13:03
  • 1
    On the other hand, $\theta_d=\frac\pi2$ should give $R_{\rm steer}=L$, $R_{\rm back}=0$ and thus different signs on the back axle speeds, as the center of rotation is now inside this axle. – Lutz Lehmann Dec 09 '21 at 13:09
  • It does make much more sense now. I looked at it as an angle because I did not know what I was looking at. Thank you. Here are the formulas, it looks like it is working correctly now. https://www.desmos.com/calculator/lbf6un5fwq Do you maybe know a software where I could simulate the robot wheels movement by any chances? By the way... What you wrote here cleared everything up for me, so it is the answer I was looking for and I can accept it as such. Thank you! – user1937747 Dec 09 '21 at 21:00

0 Answers0