Does $f(x) = \sum_{k=1}^{\infty} (-1)^{k+1} \sin(x/k)$ have infinitely many real zeros?

Question

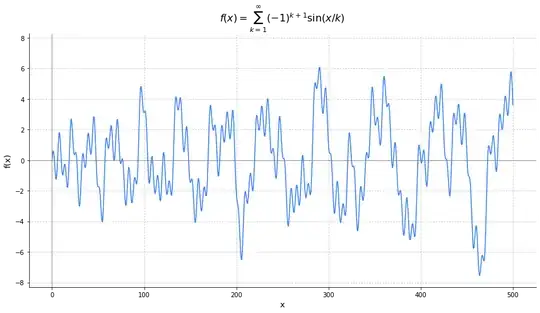
I am investigating the properties of the function $f(x)$ defined for $x \in \mathbb{C}$ by the series: $$f(x) = \sum_{k=1}^{\infty} (-1)^{k+1} \sin\left(\frac{x}{k}\right)$$

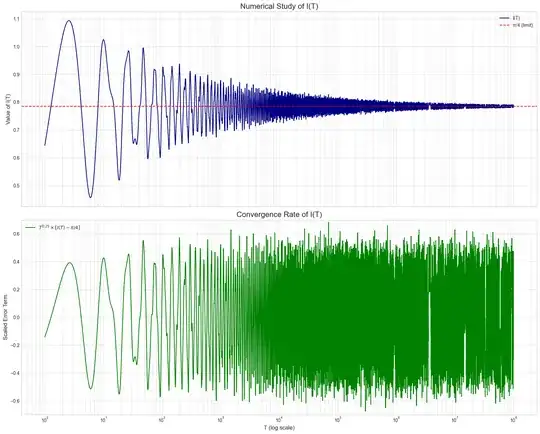
This function was the subject of a previous question on its boundedness, where it was shown to be unbounded on $\mathbb{R}$. Also numerically studies about its zeroes where conducted here.

My question is whether we can prove that $f(x)$ has infinitely many real zeros. I have summarized my current understanding of the function's properties below.

Function's properties

1. Entire Function:

   • The function $f(x)$ is entire (analytic on the whole complex plane $\mathbb{C}$).
   • Proof Idea: Each term $\sin(x/k)$ is an entire function. By pairing terms like $\sin(x/(2k-1)) - \sin(x/(2k))$ and using sum-to-product identities, the general term of the paired series can be shown to be $O(1/k^2)$ for $x$ in any compact set. Since $\sum 1/k^2$ converges, the series for $f(x)$ converges uniformly on compact subsets of $\mathbb{C}$ by the Weierstrass M-test.

2. Taylor Series Expansion:

   • Around $x=0$, the Taylor series is given by $f(x) = \sum_{j=0}^{\infty} \frac{(-1)^j \eta(2j+1)}{(2j+1)!} x^{2j+1}$, where $\eta(s)$ is the Dirichlet eta function.
   • Proof Idea: Substitute the Taylor series for $\sin(w)$. The radius of convergence is $\infty$. Note that $f'(0) = \eta(1) = \ln 2$.

3. Symmetry:

   • $f(x)$ is an odd function: $f(-x) = -f(x)$, which trivially implies $f(0)=0$.

4. Order of Growth:

   • The order of growth $\rho$ of the entire function $f(x)$ is $\rho = 1$.
   • Proof Idea: Computed using the formula $\rho = \limsup_{n\to\infty} \frac{n \log n}{-\log |a_n|}$ with the Taylor coefficients $a_{2j+1}$ and Stirling's approximation for $\log((2j+1)!)$.

5. Hadamard Factorization:

   • As an entire function of order $\rho=1$ with a simple zero at $x=0$, $f(x)$ admits the representation: $$f(x) = (\ln 2) x \prod_{j=1}^\infty \left(1 - \frac{x^2}{z_j^2}\right)$$ where $\{\pm z_j\}_{j=1}^\infty$ are the non-zero zeros of $f(x)$ in the complex plane.
   • Proof Idea: Apply Hadamard's Factorization Theorem for $\rho=1$. The odd property ensures the product combines to the form $(1-x^2/z_j^2)$. This representation implies $f(x)$ has infinitely many complex zeros $z_j$ such that the series $\sum_{j=1}^\infty |z_j|^{-2}$ converges.

6. Unboundedness on $\mathbb{R}$:

   • The function $f(x)$ is unbounded on the real line $\mathbb{R}$.
   • Proof Idea: This was shown in the post. The argument relies on assuming $|f(x)| \le M$ and reaching a contradiction. It uses a limiting orthogonality relation for the functions $\psi_k(x) = \sin(x/k)$ to show that $\limsup_{T\to\infty} \frac{1}{T}\int_0^T f(x)^2 dx$ must be infinite, contradicting the bound $M^2$.

7. Asymptotic Growth Rate on $\mathbb{R}$:

   • It seems that $|f(x)| = O(\sqrt{|x|})$ as $|x| \to \infty$.
   • Proof Idea: Use the absolutely convergent series obtained by pairing terms: $f(x) = \sum_{m=1}^{\infty} [\sin(\frac{x}{2m-1}) - \sin(\frac{x}{2m})]$. This can be rewritten as $f(x) = 2 \sum_{m=1}^{\infty} \cos\left(\frac{x(4m-1)}{4m(2m-1)}\right) \sin\left(\frac{x}{4m(2m-1)}\right)$. Split the sum at $N \approx \sqrt{|x|}$. Bound the initial part of the sum by $O(N) \approx O(\sqrt{|x|})$ and the tail by $O(|x|/N) \approx O(\sqrt{|x|})$.

8. Mean-Square Lower Bound on $\mathbb{R}$:

   • There exists a positive constant $c$ such that for all sufficiently large $T$, the function $f(x)$ satisfies the inequality: $\int_0^T f(x)^2 dx \ge \frac{c T^{3/2}}{\sqrt{\ln T}}$.
   • Proof Idea: As detailed in this answer, this property provides a strong quantitative version of unboundedness. The proof analyzes the non-negative quantity $\frac{1}{T}\int_0^T (f(x) - S_N(x))^2 dx \ge 0$ for a partial sum $S_N(x)$. This leads to a lower bound for $\int_0^T f(x)^2 dx$ in terms of $N$ and $T$, accompanied by several error terms from finite-$T$ inner products. By carefully bounding these error terms and optimizing the choice of $N$ as a function of $T$ (specifically $N \sim \sqrt{T/\ln T}$), the stated growth rate is established. This result rigorously proves that any growth exponent $\epsilon$ for $f(x)=O(x^\epsilon)$ must satisfy $\epsilon \ge 1/4$.

9. Divergence of Associated Integrals:

   • The improper integrals $\int_1^\infty |f(x)| dx$ and $\int_1^\infty \frac{|f(x)|}{x} dx$ both diverge.
   • Proof Idea: This is a key consequence of the conflict between the mean-square lower bound (Property 7) and the asymptotic upper bound (Property 8). As shown in this answer, the proof proceeds by contradiction. Assuming $\int_1^\infty \frac{|f(x)|}{x} dx$ converges, the upper bound $|f(x)| = O(\sqrt{|x|})$ implies that $\int_1^\infty \frac{f(x)^2}{x^{3/2}} dx$ must also converge. However, using integration by parts and the mean-square lower bound from Property 7, it can be shown that this same integral must diverge, which is a contradiction. Note that @Conrad in his answer has proven it with a simpler argument based "only" on the weaker results $\frac{1}{T}\int_0^Tf(x)\sin (x/k) \, dx \to (-1)^{k+1}/2$ impliying $\frac{1}{T}\int_T^{2T}f(x)\sin x \, dx \ge 1/4$ and the result. Nice !

Question

The Hadamard factorization guarantees infinitely many zeros in $\mathbb{C}$, but does not directly tell us if any of these zeros (other than $x=0$) are real. How can one prove that $f(x)$ has infinitely many real zeros ? Intuitively, a continuous, unbounded, and oscillatory function like this should cross the x-axis infinitely often. A natural approach would be to use the Intermediate Value Theorem, which would require finding a sequence of points $x_n \to \infty$ such that the sign of $f(x_n)$ alternates. However, the slow growth and complex behavior make it difficult to prove this.

Using an Integral Transform

A related post, suggested after this question was posted, offered a promising path forward. A proof can be advanced by contradiction using an integral transform. Assume $f(x)$ has a last positive zero $X_0$, so that for all $x > X_0$, $f(x)$ is either strictly positive or strictly negative. We can test these two cases with the integral $J(w) = \int_0^\infty f(t) \frac{e^{-t/w}}{t} dt$ for $w>0$. The integral is well-defined, as the singularity of the kernel at $t=0$ is removed by $f(t)/t \to \ln 2$, and the interchange of summation and integration is justifiable. The crucial property of this transform is that for large $w$, its sign is determined by the behavior of $f(t)$ on $(X_0, \infty)$. This is because the integral over $[0, X_0]$ converges to a finite constant as $w\to\infty$, while, under the hypothesis of a constant sign for $f(t)$ on $(X_0, \infty)$, the known divergence of $\int_{X_0}^\infty |f(t)|/t \, dt$ (Property 9) forces the integral $\int_{X_0}^\infty f(t)/t \, dt$ to also diverge (to either $+\infty$ or $-\infty$). The tail integral therefore dominates the head integral, and its sign dictates the sign of $J(w)$ for large $w$. An explicit calculation, by integrating the series term-by-term, yields $J(w) = \sum_{j=1}^{\infty} (-1)^{j+1} \arctan(w/j)$. By the alternating series test, this sum is strictly positive for all $w>0$. This result directly contradicts the possibility that $f(x)$ is ultimately negative. However, it is consistent with $f(x)$ being ultimately positive. The proof would be complete upon finding a second kernel whose corresponding integral transform can be shown to be negative for arbitrarily large $w$.

Answer 1

It was not my original plan to answer my own question (and I thank Conrad for all the ideas and knowledge shared through answers and comments), considering that I spent a lot of time searching for a solution already. However, quickly after posting, the related sidebar led me to this post: Why does $\zeta$ have infinitely many zeros in the critical strip?, and the ideas there, particularly the use of integral transforms with positive kernels seemed really powerful. That led me to complete the answer about the unboundedness of f with results I had proved after Conrad's answer, in order to be able to prove asymptotic dominance for some kernels, especially needing results like $\int^\infty |f(t)|/t \,dt = \infty$. In fact, it was not really required because @Conrad in his answer to the current question proved it with a much simpler argument. But, while I was looking at integral transform for $f$ (as suggested in my question), I made a numerical observation that: $$\int_0^\infty \frac{|f(t)|}{t}dt = \infty \quad \text{and} \quad \int_0^\infty \frac{f(t)}{t}dt \overset{?}{=} \frac{\pi}{4}$$

And this is definitely not possible if at some point $f$'s sign does not change, because then for all $x$ large enough, $f(x)/x$ would be equal to $|f(x)|/x$. In what follows, I will first provide a simpler proof that the integral is bounded this is enough to answer the question. And then, using more advanced techniques of exponential sums, I will prove that the integral does in fact converge to $\pi/4$ and establish a convergence rate, not fitting the observed $O(T^{-1/4})$ though, but rather $O(T^{-1/17})$.

Proof that $I(T) = \int_0^T \frac{f(t)}{t} dt$ is Bounded

The proof proceeds in four steps: first, we split the series for $I(T)$ in two parts; second and fourth, we bound the two parts of the resulting series ; fourth, we sum the two bounds and conclude.

1. Initial Split of the Integral $I(T)$

First, we express $I(T) = \int_0^T \frac{f(t)}{t} dt$ in a more convenient form. The paired series for $f(t)/t$ converges uniformly on compact sets (we even get absolute and uniform convergence on $\mathbb{R}$), which justifies interchanging summation and integration: $$ I(T) = \sum_{k=1}^{\infty} \int_0^T \frac{\sin(t/(2k-1))}{t} dt - \int_0^T\frac{\sin(t/(2k))}{t} dt = \sum_{k=1}^{\infty} \int_{T/(2k)}^{T/(2k-1)} \frac{\sin t}{t} dt $$ To analyze this series, we relate it to the full alternating series of adjacent integrals. Using simple algebraic manipulation, we can express $I(T)$ as: $$ I(T) = \frac{1}{2} \underbrace{\int_0^T \frac{\sin t}{t} dt}_{\text{Si}(T)} + \frac{1}{2} \underbrace{\sum_{k=1}^{\infty} (-1)^{k+1} \int_{T/(k+1)}^{T/k} \frac{\sin t}{t} dt}_{J(T)} $$ where $\text{Si}(T)$ is the sine integral function that converges to $\frac{\pi}{2}$ as $T \to \infty$ so that the first term converges to $\frac{\pi}{4}$. Let's focus on the second term, $J(T)$ and split it into two parts $K = \lfloor T^{\alpha} \rfloor$, with $0 < \alpha < 1$ to be chosen later: $$ J(T) = \underbrace{\sum_{k=1}^{K-1} (-1)^{k+1} \int_{T/(k+1)}^{T/k} \frac{\sin t}{t} dt}_{J_1(T)} + \underbrace{\sum_{k=K}^{\infty} (-1)^{k+1} \int_{T/(k+1)}^{T/k} \frac{\sin t}{t} dt}_{J_2(T)} $$

Note: Proving $J(T) \to 0$ would prove that $I(T) \to \frac{\pi}{4}$, and similarly $J(T) = O(T^{-1/4})$ would prove the convergence rate.

2. Bound on the Oscillatory Part: $|J_1(T)| = O(T^{2\alpha-1})$

For $J_1(T)$, we bound the sum by the sum of the absolute values of its terms. On each interval $[T/(k+1), T/k]$, the function $1/t$ is positive and decreasing. By the Second Mean Value Theorem for Integrals, for some $\xi \in [T/(k+1), T/k]$: $$ \left|\int_{T/(k+1)}^{T/k} \frac{\sin t}{t} dt\right| = \left|\frac{k+1}{T} \int_{T/(k+1)}^\xi \sin t \, dt \right| \le \frac{k+1}{T} \cdot 2 = \frac{2(k+1)}{T} $$ The sum of the absolute values is thus bounded by: $$ |J_2(T)| \le \frac{1}{2} \sum_{k=1}^{K-1} \frac{2(k+1)}{T} = \frac{1}{T} \sum_{j=2}^{K} j = \frac{1}{T}\left(\frac{K(K+1)}{2}-1\right) $$ Using $K \le T^\alpha$, we get $|J_2(T)| \le \frac{(T^\alpha)(T^\alpha+1)}{2T} =\frac{1}{2}T^{2\alpha-1} + \frac{1}{2}T^{\alpha-1}= O(T^{2\alpha-1})$.

3. Bound on the tail Part: $|J_2(T)| = O(T^{1-2\alpha})$

Define function $\phi$ on the interval $[0, 1]$ as $ \phi(u) = (-1)^{k+1}$ for $u \in \left(\frac{1}{k+1}, \frac{1}{k}\right]$ and $\phi(0) = 0$. We can express $J_2(T)$ in terms of $\phi(u)$ by a change of variables $t=Tu$: $$ J_2(T) = \sum_{k=K}^{\infty} (-1)^{k+1} \int_{1/(k+1)}^{1/k} \frac{\sin Tu}{u} du = \int_0^{1/K} \phi(u) \frac{\sin(Tu)}{u} du $$

We define $\Phi(u) = \int_0^u \phi(y)dy$ and we derive a bound for $\Phi(u)$. We can assume have $K \ge 1$, so we only need to consider $u \in [0, 1]$. There exists only one integer $N \ge 1$ such that $1/(N+1) < u \le 1/N$. The function $\phi(u)$ is constant on such interval, so $\Phi(u)$ is monotonic there. Thus, $|\Phi(u)| \le \max(|\Phi(1/N)|, |\Phi(1/(N+1))|)$. We first bound $|\Phi(1/n)|$ for any integer $n \ge 1$ leveraging the alternating series representation: $$ |\Phi(1/n)| = \left| \int_0^{1/n} \phi(t)dt \right| = \left| \sum_{k=n}^\infty \int_{1/(k+1)}^{1/k} \phi(t)dt \right| = \left| \sum_{k=n}^\infty \frac{(-1)^{k+1}}{k(k+1)} \right| \le \frac{1}{n(n+1)} $$

Substituting this into the bound (which is maximal for $N=n$) and considering that $N \ge 1/u$, we get: $$ |\Phi(u)| \le \frac{1}{N(N+1)} \le \frac{1}{(1/u+1)(1/u)} = \frac{u^2}{(1+u)} \le u^2 $$

Going back to $J_2(T)$, we use integration by parts, integrating $\phi(u)$ and differentiating $\sin(Tu)/u$: $$ J_2(T) = \left[\Phi(u)\frac{\sin(Tu)}{u}\right]_0^{1/K} - \int_0^{1/K} \Phi(u) \left(\frac{Tu\cos(Tu)-\sin(Tu)}{u^2}\right)du $$ Using $\Phi(u) \le u^2$, the boundary term at $u=0$ vanishes since $|\Phi(u)/u| \le u \to 0$ and the term at $1/K$ is bounded by $|\Phi(1/K) \frac{\sin(T/K)}{1/K}| \le 1 / K$. For the integral part, we use same inequality for $\Phi$ and $|Tu\cos(Tu)-\sin(Tu)| \le |Tu|+|\sin(Tu)| \le 2Tu$ :

$$ \left|\int_0^{1/K} \dots \right| \le \int_0^{1/K} u^2 \frac{2Tu}{u^2} du = \int_0^{1/K} 2Tu\,du = T/K^2 = T^{1-2\alpha} $$

Combining these gives the bound $|J_2(T)| \le 1/K + T/K^2 = O(T^{-\alpha} + T^{1-2\alpha}) = O(T^{1-2\alpha})$.

4. Conclusion $J(T)$ and $I(T)$ are bounded

Finally, we combine the bounds for $J_1$ and $J_2$ with $\alpha=1/2$: $$ |J(T)| \le O(T^{2\alpha-1}) + O(T^{1-2\alpha}) = O(1) $$ Thus, $J(T)$ is bounded for large $T$ and since $I(T) = J(T) + \frac{1}{2}\text{Si}(T)$ is the sum of two bounded functions, it is itself bounded, which completes the proof.

Proof that $I(T) = \int_0^T \frac{f(t)}{t} dt = \frac{\pi}{4} + O(T^{-1/17})$

The elementary bound on $J_1(T)$ is insufficient to prove convergence. A more powerful estimate is needed, for which we turn to the van der Corput method of exponential sums. The strategy is to use integration by parts on each integral in the sum defining $J_1(T)$ and then to bound the resulting main term using a highorder-derivative test.

We apply integration by parts to each integral with $u = 1/t$ and $dv = \sin(t)dt$: $$ \int_{T/(k+1)}^{T/k} \frac{\sin(t)}{t} dt = \left[-\frac{\cos(t)}{t}\right]_{T/(k+1)}^{T/k} - \int_{T/(k+1)}^{T/k} \frac{\cos(t)}{t^2} dt $$ Substituting this into the sum for $J_1(T)$ and rearranging yields:

$$J_1(T) = \underbrace{- \frac{\cos T}{T} + (-1)^{K} \frac{K}{T}\cos\frac{T}{K}}_{O(T^{\alpha-1})} + \frac{2}{T} \underbrace{\sum_{k=2}^{K-1} (-1)^k k \cos\frac{T}{k}}_{S_A(T)} - \underbrace{\sum_{k=1}^{K-1} (-1)^{k+1} \int_{T/(k+1)}^{T/k} \frac{\cos(t)}{t^2} dt}_{S_B(T)} $$

First, we bound the error sum $S_B(T)$. Since $t \in [T/(k+1), T/k]$, we can bound the integral using the Second Mean Value Theorem for Integrals: $$ \left|\int_{T/(k+1)}^{T/k} \frac{\cos(t)}{t^2} dt\right| = \frac{(k+1)^2}{T^2} \left| \int_{T/(k+1)}^{\xi} \cos(t) dt \right| \le 2 \frac{(k+1)^2}{T^2} $$ for some $\xi \in [T/(k+1), T/k]$. Summing these bounds gives: $$ |S_B(T)| \le \sum_{k=1}^{K-1} \frac{2(k+1)^2}{T^2} = \frac{K(K+1)(2K+1)}{3T^2} = O(T^{3\alpha-2}) $$

Next we address $S_A(T)$, that can be rewritten as real part of a complex exponential sum: $S_A(T)=\text{Re} \left( \sum_{k=2}^{K-1} k \, e^{i(\pi k + T/k)} \right)$, and bounding it by bounding it's magnitude. Let $A(n) = \sum_{k=2}^n e^{i(\pi k + T/k)}$. Then the sum in question is $\sum_{k=2}^{K-1} k \, e^{i(\pi k + T/k)}$, which by summation by parts is:

$$ \sum_{k=2}^{K-1} k \, e^{i(\pi k + T/k)} = (K-1)A(K-1) - \sum_{k=2}^{K-2} A(k) $$

The problem is now to bound the unweighted exponential sum $A(n) = \sum_{k=2}^n e^{2 i \pi g(k)}$ where $g(x) = x/2 + T/(2\pi x)$. To do that, we use Theorem 2.6 from Graham and Kolesnik's book on exponential sums to bound the sum on dyadic intervals. Let $I_N = [N, 2N-1]$ be a subinterval of $[2, n]$. We verify the hypotheses of the theorem:

1. $g(x)$ has three continuous derivatives. Its derivatives are $g'(x) = 1/2 - T/(2\pi x^2)$, $g''(x) = T/(\pi x^3)$, and $g'''(x) = -3T/(\pi x^4)$.
2. There exist $\lambda > 0$ and $\alpha > 1$ such that $\lambda \le |g'''(x)| \le \alpha\lambda$ on $I_N$. The function $|g'''(x)|$ is positive and decreasing on $I_N$. Thus we have $\frac{3T}{\pi (2N-1)^4} \le |g'''(x)| \le \frac{3T}{\pi N^4}$. We can choose $\lambda = \frac{3T}{\pi (2N-1)^4}$. Then $|g'''(x)| \le \frac{3T}{\pi N^4} = \left(\frac{2N-1}{N}\right)^4 \lambda$. For $N \ge 1$, this factor is less than $16$, so we can take $\alpha = 16$.

With the hypotheses satisfied, Theorem 2.6 gives the following bound for the sum over $I_N$, which has length $|I_N| = N$: $$ \left| \sum_{k=N}^{2N-1} e^{2i\pi g(k)} \right| =O \left( N\lambda^{1/6} + N^{3/4} + N^{1/4}\lambda^{-1/4} \right) = O \left( T^{1/6}N^{1/3} + N^{3/4} + T^{-1/4}N^{5/4} \right) $$

To find the bound for $|A(n)|$, we sum the bounds over the dyadic intervals that partition $[2, n]$. This sum is dominated by the largest value of $N \approx n$: $$ |A(n)| = O \left( T^{1/6}n^{1/3} + n^{3/4} + T^{-1/4}n^{5/4} \right) $$

Now we use this to bound $|S_A(T)| \le (K-1)|A(K-1)| + \sum_{k=2}^{K-2} |A(k)|$. We have:

$$ \left| S_A(T) \right| = O \left( T^{1/6}K^{4/3} + K^{7/4} + T^{-1/4}K^{9/4} + \sum_{k=2}^{K-2} \left(T^{1/6}k^{1/3} + k^{3/4} + T^{-1/4}k^{5/4}\right) \right) $$

The sum can be bounded by the corresponding integral: $\int_1^{K-1} \left(T^{1/6}x^{1/3} + x^{3/4} + T^{-1/4}x^{5/4}\right) dx = O\left(T^{1/6}K^{4/3} + K^{7/4} + T^{-1/4}K^{9/4}\right)$, therefore: $$ \frac{2}{T} |S_A(T)| = O \left( T^{-5/6}K^{4/3} + T^{-1}K^{7/4} + T^{-5/4}K^{9/4} \right) = O \left( T^{4\alpha/3 - 5/6} + T^{7\alpha/4 - 1} + T^{9\alpha/4 - 5/4} \right) $$

Combining bounds for boundary terms, $S_A(T)$, and $S_B(T)$: $$ |J_1(T)| = O \left( T^{\alpha-1} + T^{4\alpha/3 - 5/6} + T^{7\alpha/4 - 1} + T^{9\alpha/4 - 5/4} + T^{3\alpha-2} \right) $$ The optimal choice of $\alpha$ will balance these exponents to achieve the best decay rate. We can now collect all error terms for

$$J(T) = J_1(T) + J_2(T) = O\left( T^{\alpha-1} + T^{4\alpha/3 - 5/6} + T^{7\alpha/4 - 1} + T^{9\alpha/4 - 5/4} + T^{3\alpha-2} + T^{1-2\alpha} \right) $$

For convergence, all exponents must be negative. This requires $\alpha \in (1/2, 5/9)$. To find the optimal rate, we balance the dominant error terms by equating the exponents that define the boundaries of this interval $9\alpha/4 - 5/4$ and $1 - 2\alpha$. Setting these equal gives $\alpha = 9/17$. With this choice, both dominant exponents become $1-2(9/17) = -1/17$. Thus, the total error for $J(T)$ is bounded by: $$ |J(T)| = O(T^{-1/17}) $$ Finally, we return to the original integral $I(T)$: $$ I(T) = \frac{1}{2} \text{Si}(T) + \frac{1}{2}J(T) $$ Using the known asymptotic expansion for the sine integral, $\text{Si}(T) = \frac{\pi}{2} + O(T^{-1})$, we obtain the final result: $$ I(T) = \frac{1}{2}\left(\frac{\pi}{2} + O(T^{-1})\right) + \frac{1}{2}O(T^{-1/17}) = \frac{\pi}{4} + O(T^{-1/17}) $$

Answer 2

Let's assume by contradiction that $f$ has only finitely many zeroes, so $f(x)$ is of constant sign for $x \ge a$. As the OP proved, it then follows that $f(x)>0, x \ge a$ so we will treat only this case by a deeper study of the OP method.

Since the proof is fairly long and uses my previous answer in the linked post below and the OP's ideas above let me present a Short Overview first:

The idea is that if $g(x)=f(x)-\sin x$ then $f,g$ are "close" as $|g| \le |f| +1$ while also $\int_T^{2T}\frac{f(x)-g(x)}{x} \to 0, T \to \infty$ and they satisfy the absolute relations $$|\int_{T_0}^Tf(x)dx| \le cT, |\int_{T_0}^Tg(x)dx| \le cT$$ $$\int_{T}^{2T}|f(x)|dx \ge c_1T, \int_{T}^{2T}|g(x)|dx \ge c_1T$$

Using positivity for $f$ (and the fact that $g$ is close to $f$) we can prove that for some fixed $a$ and all large $T$ $$\int_a^T f(x)/xdx \ge c_2\log T/a, \int_a^T g(x)/xdx \ge c_2\log T/a$$

However the integral against the nucleus $\frac{e^{-xw}}{x}, w>0$ is positive for $f$ and negative for $g$ and since for $w \to 0$ the integrals (at least on finite segments) correspond to $f(x)/x, g(x)/x$ which are close and large under the assumptions of $f$ positive we get the required contradiction to the positivity of $f$.

Here are the details

First let's note that we proved in the previous related post $$\frac{1}{T}\int_0^Tf(x)\sin (x/k) dx \to (-1)^{k+1}/2$$ hence $$\frac{1}{T}\int_T^{2T}f(x)\sin (x/k) dx \to (-1)^{k+1}/2$$ which (using $k=1$) implies that for $T \ge a_1 >a$ large enough $$\frac{1}{T}\int_T^{2T}f(x)\sin x dx \ge 1/4$$ so $$\frac{1}{4} \le |\frac{1}{T}\int_T^{2T}f(x)\sin x dx| \le \frac{1}{T}\int_T^{2T}|f(x)|dx$$

In particular for $T>a_1>1$ we have $$\int_T^{2T}\frac{|f(x)|}{x}dx \ge \frac{1}{2T}\int_T^{2T}|f(x)|dx \ge \frac{1}{8}$$ which trivially impiles the divergence of the integral $\int_1^\infty \frac{|f(x)|}{x} dx$

By our assumption $|f(x)|=f(x), x \ge a_1$ so for $T \ge a_1$ we have $$\int_T^{2T}\frac{f(x)}{x}dx \ge \frac{1}{8}$$

Now consider $g(x)=f(x)-\sin x$ and note that since $\int_0^{\infty}\frac{\sin (x)}{x}dx$ converges we have $\int_T^{2T}\frac{\sin x}{x}dx \to 0, T \to \infty$ so for $T \ge a_2>a_1$ we have $$\int_T^{2T}\frac{g(x)}{x}dx =\int_T^{2T}\frac{f(x)}{x}dx-\int_T^{2T}\frac{\sin (x)}{x}dx \ge \frac{1}{16}$$

Taking large $T> 4a_3$ and using diadic splits $T, T/2,...T/2^k \ge a_3 >T/2^{k+1}$ so $k \ge \log_2 (T/a_3)-1 \ge \frac{1}{2}\log_2 (T/a_3)$ we get that $$\int_{a_3}^T \frac{g(x)}{x} dx \ge \frac{1}{32}\log_2 (T/a_3)= C\log (T/a_3)$$

We will prove below that (independently on any assumption about the positivity of $f$) that $$|\int_{T_0}^Tf(x)dx| \le K_1T$$ for $T>T_0 \ge a_3 >a_2$ so since $f(x)=|f(x)|$ there, $\int_{T_0}^T|f(x)|dx \le K_1T$ and as before (in the case $f \ge 0, x \ge a_3$ though only as here we need to take out the denominator and that is valid only for $f \ge 0$) $\int_T^{2T}f(x)/xdx \le 2K_1$. But $|g(x)| \le |f(x)|+1$ which implies that $\int_{T_0}^T|g(x)|dx \le K_2T$

Now by the OP computation we have $$J_1(w) = \int_0^\infty g(x) \frac{e^{-xw}}{x} dx=\sum_{j=2}^{\infty} (-1)^{j+1} \arctan(1/(wj)) <0, w >0$$ and we will derive a contradiction as follows. Take $T$ large, $w=T^{-1}$, and $A= \int_0^{a_3} \frac{|g(x)|}{x}dx <\infty$ as in the OP and write $$J_1(w)=(\int_0^{a_3}+\int_{a_3}^T+\int_{T}^{\infty})g(x) \frac{e^{-xw}}{x} dx$$ and we will estimate each integral $I_1,I_2, I_3$ as follows

$I_1 \le A$, while for $I_3$ we use $|g(x)| \le |f(x)|+1$ so $$|\int_{T}^{\infty}g(x) \frac{e^{-xw}}{x}dx| \le \int_{T}^{\infty}f(x) \frac{e^{-xw}}{x}dx+\int_{T}^{\infty}\frac{e^{-xw}}{x}dx$$

Now using $xw=y, \frac{dx}{x}=\frac{dy}{y}, Tw=1$ we have $$\int_{T}^{\infty}\frac{e^{-xw}}{x}dx=\int_{1}^{\infty}\frac{e^{-y}}{y}dx=C_1$$ while splitting $[T, \infty)$ diadically and noting that $e^{-xw} \le e^{-2^k}, x \in [2^kT, 2^{k+1}T]$ we get $$\int_{T}^{\infty}f(x) \frac{e^{-xw}}{x}dx \le 2K_1(e^{-1}+e^{-2}+e^{-4}+...) \le K_3$$

Using $1-e^{-xw} \le xw$ we have that $|I_2-\int_{a_3}^{T}\frac{g(x)}{x}dx| \le w\int_{a_3}^{T}|g(x)|dx \le K_2wT=K_2$ so $$I_2 \ge \int_{a_3}^{T}\frac{g(x)}{x}dx-K_2 \ge C \log (T/a_3)-K_2$$

Putting everything together we get $$J_1(w) \ge I_2-|I_1|-|I_3| \ge C \log (T/a_3)-K_4>0$$ if $T$ large enough and that is the required contradiction with $J_1(w)=\sum_{j=2}^{\infty} (-1)^{j+1} \arctan(1/(wj)) <0$

We will now sketch the proof of $$|\int_{T_0}^Tf(x)dx| \le K_1T$$ or by integrating term by term we need to prove that if $$S(T)=\sum_{n=1}^{\infty}(-1)^{n+1} n(1-\cos T/n)$$ then $|S(T)| \le K_5T$ since applying it with $T_0, T$ gives $$|\int_{T_0}^Tf(x)dx|=|\int_{0}^Tf(x)-\int_0^{T_0}f(x)dx|=|S(T)-S(T_0)| \le 2K_5T$$

We split the $S(T)$ in ranges $1 \le n \le \sqrt T, \sqrt T < n \le T+1, n > T+1$

Now $1-\cos T/n=2\sin^2 T/(2n)$ and since $\sin^2 x=\sum a_k x^k$ entire we have $|a_k| \le C_2$ and we can write $\sin ^2 x=\sum_{2 \le k \le N}a_k x^k+R(x)$ and $|R(x)| \le C_2|x|^{N+1}\frac{1}{1-|x|} \le 2C_2|x|^{N+1}, |x| \le 1/2$ while $|\sum_{n >T+1}(-1)^{n+1}2n\frac{T^k}{(2n)^k}| \le T (\frac{T}{2T+2})^{k-1} \le T2^{1-k}, k=2,...N$ since the terms are positive decreasing hence the first term dominates in absolute value in the alternating sum ($c_m$ decreases to $0$ then $|\pm (c_1-c_2+c_3-c_4...)| \le c_1$). In particular using $|a_k|\le C_2$ we get that part at most $C_2T \sum_{k \ge 2}2^{1-k} \le C_2T$ and the error which we need majorize by absolute value is clearly at most $2C_2T^{2}\sum_{n \ge T+1}(T/(2n))^{N-1} \le 2^{2-N}C_2T^{N+1}\int_T^{\infty}x^{1-N}=2^{2-N}C_2T^2/(N-1)$. In particular, we can choose $N$ large enough so $2^{2-N}T^2<1$ and this term is inconsequential.

For the range $T^{1/2} \le n \le T+1$ we note that $\sum \pm n=O(T)$ and apply Kuzmin Landau to $R_{m,M}=\sum_{n \le m \le k \le M \le T+1}\pm \cos T/k=O(1)$ indepedently of $n,m,M,T$ as shown in the linked post so by partial summation we get $O(T)$ again for our sum, while in the range $n \le \sqrt T$ we majorize each term trivially by $2n$ and $\sum_{ 1 \le n \le \sqrt T}(2n)=O(T)$ and we are done!

Note that if we could prove that $\int_T^{2T}|f(x)|dx>>T^{1+\epsilon}$ for some $\epsilon>0$ and a sequence at least of $T \to \infty$ we wouldn't need all the complications above since $\int_T^{2T}f(x)dx=O(T)$ but I do not see how to show that - my expectation is the above holds since $|f|$ should be large (at least $|x|^{\epsilon}$ for $\epsilon \le 1/4$ quite often). Also, note that the result $\int_T^{2T}|f(x)|dx \ge cT$ is independent on any positivity assumptions so another idea - which I thought originally to hold - is if we can show that $\int_T^{2T}f(x)dx=o(T)$ again at least for a sequence of $T \to \infty$ but I came to believe (though I do not have a proof but feels right by analogy with the divisor problem) that there are $T \to \infty$ for which $\int_T^{2T}f(x)dx >>T$ so a general proof of $\int_T^{2T}f(x)dx=o(T)$ based on exponential sums cannot hold directly, though another averaging on $T$ may work...