What is the geometric locus of point $M$ that makes point $Z$ the middle of points $X,Y$

Question

Yesterday, while playing around with the GeoGebra application, I discovered a beautiful property of conic sections:

Theorem (Direct Statement)

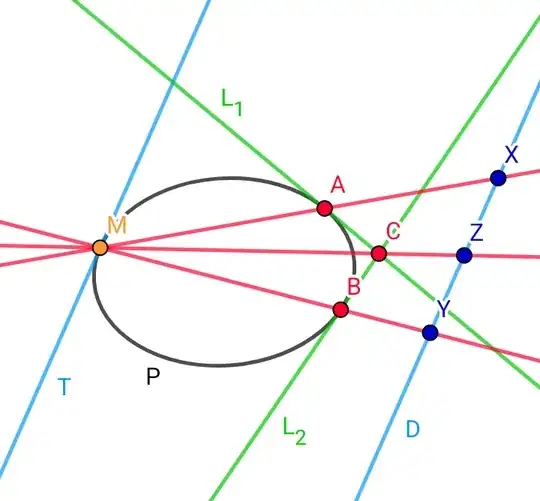
Given: Let $H$ be a plane, and let $P$ be a conic section lying in $H$. Let $D$ be a line in $H$. Let $L_1$ and $L_2$ be tangents to $P$ at points $A$ and $B$, respectively, and suppose they intersect at point $C$. Let $T$ be a line parallel to $D$ and tangent to $P$ at a point $M$. Let $X = AM \cap D$, $Y = BM \cap D$, and $Z = CM \cap D$.

Claim: Point $Z$ is the midpoint of segment $XY$.

---

Converse Statement

After further reflection, I realized that the converse of this theorem also seems to hold. It can be stated as follows:

Given: Let $H$ be a plane, and let $P$ be a conic section in $H$. Let $D$ be a line in $H$. Let $L_1$ and $L_2$ be tangents to $P$ at points $A$ and $B$, respectively, intersecting at point $C$. Let $T$ be a tangent to $P$ at point $M$ (not necessarily parallel to $D$). Let $X = AM \cap D$, $Y = BM \cap D$, and $Z = CM \cap D$, with the additional condition that $Z$ is the midpoint of segment $XY$.

Claim: Lines $T$ and $D$ are parallel.

---

My Questions:

Q1: How can we prove the direct theorem stated above?

Q2: Is this theorem known in the literature? If so, could you kindly provide a reference where it is mentioned?

Q3: This theorem implies that there are infinitely many points $M$ in $H$ satisfying the condition (since there are infinitely many conics through $A$ and $B$ with $L_1$ and $L_2$ as tangents). What is the locus of such points $M$ that preserve the midpoint condition for $Z$? Can this locus be constructed from the data of $A$, $B$, $C$, and the line $D$?

---

Note 1:

You may help me answer this question if you can suggest a method for constructing a conic tangent to two given lines at two known points and passing through a third known point (all in the same plane), using only ruler and compass. (By “constructing a conic with ruler and compass,” I mean: either constructing its key elements such as foci and vertices, or constructing two additional points on the conic — because I already know how to construct a conic through five points using classical tools. See my question and answer on this topic.)

---

Note 2:

I know how to construct a parabola tangent to two given lines at two given points, using the so-called Steiner generation of a parabola. Therefore, I can construct one point on the locus of $M$. However, I don’t know how to construct any of the other conics tangent to $L_1$ and $L_2$ at $A$ and $B$, respectively. If you can tell me how to construct such a conic, it would be extremely helpful.

Answer 1

For the direct statement, with a bit of projective geometry:

Use an arbitrary projective transformation of the plane which sends the line $T$ to the line at infinity. Notice that the point of $D$ which is at infinity is the intersection of $D$ and $T$, so it remains at infinity after the transformation. This means that the transformation of $D$ is actually affine, so $Z$ will be in the middle of $XY$ after the transformation iff it was in the middle before.

The transformation sends the conic to a parabola, say to $y = x^2$, and the lines passing through $M$ are now (transformed to) vertical lines. We can still use an affine transformation of the plane, preserving our parabola $y=x^2$, to move $C$ to the $y$-axis. Then, by symmetry, $A = (x, x^2)$ and $B = (-x, x^2)$ for a suitable $x$, and so the 3 vertical lines passing through $A, C, B$ are equidistant, hence any line, in particular $D$, will intersect them in points $X, Z, Y$ s.t. $Z$ is in the middle of $XY$.

Edit: How to get the promised affine transformation of the plane moving $C$ to the $y$ axis: For any number $a$ the affine transformation of the plane $(x, y)\mapsto (x + a, y + 2ax + a^2)$ preserves the parabola $y = x^2$. We simply choose $a$ so that the $x$-coordinate of $C$ becomes $0$.

Answer 2

The method used by user8268 is good. Indeed, we can send $M$ to infinity, making the conic curve a parabola.

We use for that a certain projective transform making lines $AX, BY, CZ$ parallel and line $D$, being parallel to the tangent at infinity, orthogonal to those 3 lines, a parallel to the directrix ; besides, as the point at infinity $P_{\infty}$ of line $D$ remains fixed, so the cross-ratio $(P_{\infty},Z;Y,X)$ is also fixed ; if it is $-1$ before, in the case of a midpoint, it will remain $-1$ after the transformation.

Here is a proof differing from the previous one by the fact that we don't use the assumption that $A$ and $B$ have to be symmetrical with respect to the axis of the parabola.

Indeed, consider that this transformed parabola has, with respect to "ad hoc" axis the

• cartesian equation

$$y=\tfrac{1}{4a}x^2\tag{1}$$

• or (equivalent) parametric equations

$$P_t=(x=2at, y=at^2)\tag{2}$$

A small calculation shows that tangent lines to parabola in $A=P_{t_1}$ and $B=P_{t_2}$ meet in point $C$ with coordinates :

$$C=(a(t_1+t_2),at_1t_2)\tag{3}$$

(sanity check : consider the limit case $t_1=t_2=t$ in (3), one retrieves (2).)

Now take $a=\tfrac12$ : $C$ (and therefore $Z$) has abscissa $\tfrac12(t_1+t_2)$ with points $A=P_{t_1}$ and $B=P_{t_2}$ with resp. abscissas $t_1,t_2$ (which are also the abscissas of $X$ and $Y$ resp.)

Finished.